Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 127, pp. 1-9.
Positive solutions for a system of nonlinear
boundary-value problems on time scales
A. Kameswara Rao
Abstract:
We determine the values of a parameter
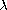 for which there
exist positive solutions to the system of dynamic equations
for which there
exist positive solutions to the system of dynamic equations
![$$\displaylines{
u^{\Delta \Delta}(t)+\lambda p(t)f(v(\sigma(t)))=0,\quad
t\in[a, b]_\mathbb{T}, \cr
v^{\Delta \Delta}(t)+\lambda q(t)g(u(\sigma(t)))=0,
\quad t\in[a, b]_\mathbb{T},
}$$](gifs/ab.gif)
with the boundary conditions,
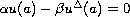 ,
,
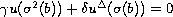 ,
,
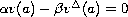 ,
,
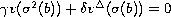 ,
where
,
where
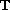 is a time scale. To this end we apply
a Guo-Krasnosel'skii fixed point theorem.
is a time scale. To this end we apply
a Guo-Krasnosel'skii fixed point theorem.
Submitted July 6, 2009. Published October 4, 2009.
Math Subject Classifications: 39A10, 34B15, 34A40.
Key Words: Dynamic equations; eigenvalue intervals;
positive solution; cone.
Show me the PDF file (209 KB),
TEX file for this article.
A. Kameswara Rao
Department of Applied Mathematics, Andhra University
Visakhapatnam 530 003, India
email: kamesh_1724@yahoo.com
|
Return to the EJDE web page
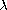 for which there
exist positive solutions to the system of dynamic equations
for which there
exist positive solutions to the system of dynamic equations
![$$\displaylines{
u^{\Delta \Delta}(t)+\lambda p(t)f(v(\sigma(t)))=0,\quad
t\in[a, b]_\mathbb{T}, \cr
v^{\Delta \Delta}(t)+\lambda q(t)g(u(\sigma(t)))=0,
\quad t\in[a, b]_\mathbb{T},
}$$](gifs/ab.gif)
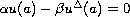 ,
,
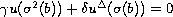 ,
,
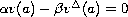 ,
,
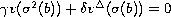 ,
where
,
where
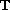 is a time scale. To this end we apply
a Guo-Krasnosel'skii fixed point theorem.
is a time scale. To this end we apply
a Guo-Krasnosel'skii fixed point theorem.