Electron. J. Diff. Equ.,
Vol. 2009(2009), No. 128, pp. 1-9.
Homoclinic solutions for a class of second order
non-autonomous systems
Rong Yuan, Ziheng Zhang
Abstract:
This article concerns the existence of homoclinic solutions
for the second order non-autonomous system
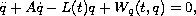
where
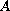 is a skew-symmetric constant matrix,
is a skew-symmetric constant matrix,
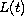 is a symmetric
positive definite matrix depending continuously on
is a symmetric
positive definite matrix depending continuously on
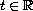 ,
,
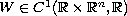 .
We assume that
.
We assume that
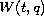 satisfies the global Ambrosetti-Rabinowitz
condition, that the norm of A is sufficiently small and
that
satisfies the global Ambrosetti-Rabinowitz
condition, that the norm of A is sufficiently small and
that
 and
and
 satisfy additional hypotheses. We prove the
existence of at least one nontrivial homoclinic solution, and
the existence of infinitely many homoclinic solutions if
satisfy additional hypotheses. We prove the
existence of at least one nontrivial homoclinic solution, and
the existence of infinitely many homoclinic solutions if
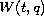 is even in
is even in
 .
Recent results in the literature are generalized and improved.
.
Recent results in the literature are generalized and improved.
Submitted October 14, 2008. Published October 7, 2009.
Math Subject Classifications: 34C37, 35A15, 37J45.
Key Words: Homoclinic solutions; critical point; variational methods;
mountain pass theorem.
Show me the PDF file (234 KB),
TEX file for this article.
 |
Rong Yuan
School of Mathematical Sciences, Beijing Normal University
Laboratory of Mathematics and Complex Systems, Ministry of Education
Beijing 100875, China
email: ryuan@bnu.edu.cn
|
|---|
 |
Ziheng Zhang
School of Mathematical Sciences, Beijing Normal University
Laboratory of Mathematics and Complex Systems, Ministry of Education
Beijing 100875, China
email: zhzh@mail.bnu.edu.cn
|
|---|
Return to the EJDE web page
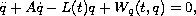
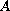 is a skew-symmetric constant matrix,
is a skew-symmetric constant matrix,
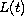 is a symmetric
positive definite matrix depending continuously on
is a symmetric
positive definite matrix depending continuously on
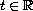 ,
,
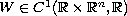 .
We assume that
.
We assume that
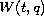 satisfies the global Ambrosetti-Rabinowitz
condition, that the norm of A is sufficiently small and
that
satisfies the global Ambrosetti-Rabinowitz
condition, that the norm of A is sufficiently small and
that
 and
and
 satisfy additional hypotheses. We prove the
existence of at least one nontrivial homoclinic solution, and
the existence of infinitely many homoclinic solutions if
satisfy additional hypotheses. We prove the
existence of at least one nontrivial homoclinic solution, and
the existence of infinitely many homoclinic solutions if
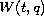 is even in
is even in
 .
Recent results in the literature are generalized and improved.
.
Recent results in the literature are generalized and improved.

