Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 14, pp. 1-5.
Boundedness of solutions for a Lienard
equation with multiple deviating arguments
Yuehua Yu, Changhong Zhao
Abstract:
We consider the Lienard equation
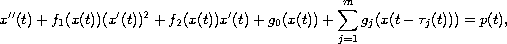
where
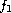 ,
,
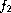 ,
,
 and
and
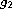 are continuous
functions, the delays
are continuous
functions, the delays
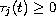 are bounded continuous,
and
are bounded continuous,
and
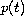 is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
Submitted December 15, 2008. Published January 13, 2009.
Math Subject Classifications: 34C25, 34K13, 34K25.
Key Words: Lienard equation; deviating argument; bounded solution.
Show me the PDF file (187 KB),
TEX file for this article.
Yuehua Yu
Department of Mathematics
Hunan University of Arts and Science
Changde, Hunan 415000, China
email: jinli127@yahoo.com.cn |
Changhong Zhao
Department of Mathematics
Hunan University of Arts and Science
Changde, Hunan 415000, China
email: hongchangzhao@yahoo.com.cn |
Return to the EJDE web page
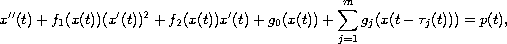
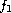 ,
,
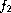 ,
,
 and
and
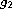 are continuous
functions, the delays
are continuous
functions, the delays
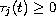 are bounded continuous,
and
are bounded continuous,
and
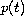 is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.
is a bounded continuous function.
We obtain sufficient conditions for all solutions and
their derivatives to be bounded.