Electron. J. Diff. Equ., Vol. 2009(2009), No. 163, pp. 1-9.

Three positive solutions for a system of singular generalized Lidstone problems

Jiafa Xu, Zhilin Yang

Abstract:
In this article, we show the existence of at least three positive solutions for the system of singular generalized Lidstone boundary value problems
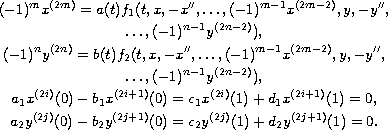
$$\displaylines{ (-1)^m x^{(2m)}=a(t)f_1(t,x,-x'',\dots,(-1)^{m-1}x^{(2m-2)},y,-y'',\cr \dots,(-1)^{n-1}y^{(2n-2)}), \cr (-1)^n y^{(2n)}=b(t)f_2(t,x,-x'',\dots,(-1)^{m-1}x^{(2m-2)},y,-y'',\cr \dots,(-1)^{n-1}y^{(2n-2)}), \cr a_1 x^{(2i)}(0)-b_1 x^{(2i+1)}(0)=c_1x^{(2i)}(1)+d_1 x^{(2i+1)}(1)=0,\cr a_2y^{(2j)}(0)-b_2y^{(2j+1)}(0)=c_2y^{(2j)}(1)+d_2y^{(2j+1)}(1)=0. }$$
The proofs of our main results are based on the Leggett-Williams fixed point theorem. Also, we give an example to illustrate our results.

Submitted October 7, 2009. Published December 21, 2009.
Math Subject Classifications: 34A34, 34B18, 45G15, 47H10.
Key Words: Singular generalized Lidstone problem; positive solution; cone; concave functional.

Show me the PDF file (192 KB), TEX file for this article.

Jiafa Xu
Department of Mathematics, Qingdao Technological University
No 11, Fushun Road, Qingdao, China
email: xujiafa292@sina.com
Zhilin Yang
Department of Mathematics, Qingdao Technological University
No 11, Fushun Road, Qingdao, China
email: zhilinyang@sina.com

Return to the EJDE web page