We are interested in the existence of positive solutions to a four-point boundary value problem of the differential equation
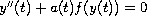on
![$ [0,1] $](gifs/ab.gif)
.
The value of
at 0 and 1 are each a multiple of
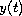at an interior point.
Many known existence criteria are based on the limiting values
of
as
approaches
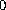and infinity.
In this article we obtain an optimal criterion (thereby improving all existing results of kind mentioned above) by comparing these limiting values to the smallest eigenvalue of the corresponding four-point problem of the associated linear equation. In the simpler case of three-point boundary value problems, the same result has been established in an earlier paper by the first author using the shooting method.
The method of proof is based upon a variant of Krasnoselskii's fixed point theorem on cones, the classical Krein-Rutman theorem, and the Gelfand formula relating the spectral radius of a linear operator to its norm.
