This article concerns the the nonlinear elliptic equation
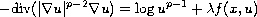
in a bounded domain
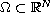 with
with
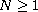 and
and
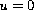 on
on
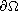 .
By means of a double
perturbation argument, we obtain a nonnegative solution.
.
By means of a double
perturbation argument, we obtain a nonnegative solution.
Jing Mo, Zuodong Yang
Abstract:
This article concerns the the nonlinear elliptic equation
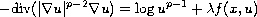
in a bounded domain
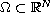 with
with
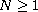 and
and
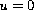 on
on
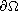 .
By means of a double
perturbation argument, we obtain a nonnegative solution.
.
By means of a double
perturbation argument, we obtain a nonnegative solution.
Submitted February 23, 2009. Published July 10, 2009.
Math Subject Classifications: 35B20, 35B65, 35J65.
Key Words: Existence; logarithmic nonlinearity; supersolution;
subsolution.
Show me the PDF file (225 KB), TEX file for this article.
| Jing Mo Institute of Mathematics, School of Mathematics Science Nanjing Normal University Jiangsu Nanjing 210097, China email: jingshuihailang@163.com | |
 |
Zuodong Yang Institute of Mathematics, School of Mathematics Science Nanjing Normal University Jiangsu Nanjing 210097, China email: zdyang_jin@263.net |
Return to the EJDE web page