Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 90, pp. 1-15.
Second-order boundary estimates for solutions to
singular elliptic equations
Claudia Anedda
Abstract:
Let
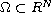 be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
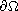 in the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the singular semilinear
equation
in the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the singular semilinear
equation
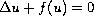 .
Under appropriate growth conditions on
.
Under appropriate growth conditions on
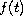 as
as
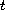 approaches zero, we find an asymptotic expansion up
to the second order of the solution in terms of the distance from
approaches zero, we find an asymptotic expansion up
to the second order of the solution in terms of the distance from
 to the boundary
to the boundary
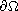 .
.
Submitted June 17, 2009. Published July 30, 2009.
Math Subject Classifications: 35B40, 35B05, 35J25.
Key Words: Elliptic problems; singular equations;
second order boundary approximation.
Show me the PDF file (251 KB),
TEX file for this article.
 |
Claudia Anedda
Dipartimento di Matematica e Informatica
Universitá di Cagliari
Via Ospedale 72, 09124 Cagliari, Italy
email: canedda@unica.it
|
|---|
Return to the EJDE web page
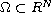 be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
be a bounded smooth domain.
We investigate the effect of the mean curvature of the boundary
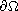 in the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the singular semilinear
equation
in the behaviour of the solution to the homogeneous
Dirichlet boundary value problem for the singular semilinear
equation
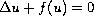 .
Under appropriate growth conditions on
.
Under appropriate growth conditions on
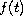 as
as
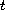 approaches zero, we find an asymptotic expansion up
to the second order of the solution in terms of the distance from
approaches zero, we find an asymptotic expansion up
to the second order of the solution in terms of the distance from
 to the boundary
to the boundary
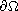 .
.
