Electron. J. Diff. Eqns.,
Vol. 2009(2009), No. 91, pp. 1-17.
Distribution-valued weak solutions to a parabolic
problem arising in financial mathematics
Michael Eydenberg, Maria Cristina Mariani
Abstract:
We study distribution-valued solutions to a parabolic problem that
arises from a model of the Black-Scholes equation in option pricing.
We give a minor generalization of known existence and uniqueness
results for solutions in bounded domains
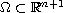 to give existence of solutions
for certain classes of distributions
to give existence of solutions
for certain classes of distributions
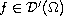 .
We also study growth conditions for smooth solutions of certain
parabolic equations on
.
We also study growth conditions for smooth solutions of certain
parabolic equations on
 that have
initial values in the space of distributions.
that have
initial values in the space of distributions.
Submitted September 10, 2008. Published July 30, 2009.
Math Subject Classifications: 35K10, 35D30, 91B28.
Key Words: Weak solutions; parabolic differential equations;
Black-Scholes type equations.
Show me the PDF file (298 KB),
TEX file for this article.
| |
Michael Eydenberg
Department of Mathematical Sciences
New Mexico State University
Las Cruces, NM 88003-8001, USA
email: mseyden@nmsu.edu
|
|---|
 |
María Cristina Mariani
Department of Mathematical Sciences
University of Texas, El Paso, Bell Hall 124
El Paso, Texas 79968-0514, USA
email: mcmariani@utep.edu |
|---|
Return to the EJDE web page
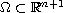 to give existence of solutions
for certain classes of distributions
to give existence of solutions
for certain classes of distributions
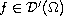 .
We also study growth conditions for smooth solutions of certain
parabolic equations on
.
We also study growth conditions for smooth solutions of certain
parabolic equations on
 that have
initial values in the space of distributions.
that have
initial values in the space of distributions.
