Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 06, pp. 1-19.
Slow and fast systems with Hamiltonian reduced problems
Maamar Benbachir, Karim Yadi, Rachid Bebbouchi
Abstract:
Slow and fast systems are characterized by having some of the derivatives
multiplied by a small parameter
 .
We study systems of reduced
problems which are Hamiltonian equations, with or without a slowly varying
parameter. Tikhonov's theorem gives approximate solutions for times of order
1. Using the stroboscopic method, we give approximations for time of order
.
We study systems of reduced
problems which are Hamiltonian equations, with or without a slowly varying
parameter. Tikhonov's theorem gives approximate solutions for times of order
1. Using the stroboscopic method, we give approximations for time of order
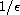 .
More precisely, the variation of the total energy of the
problem, and the eventual slow parameter, are approximated by a certain
averaged differential equation. The results are illustrated by some
numerical simulations. The results are formulated in classical mathematics
and proved within internal set theory which is an axiomatic approach to
nonstandard analysis.
.
More precisely, the variation of the total energy of the
problem, and the eventual slow parameter, are approximated by a certain
averaged differential equation. The results are illustrated by some
numerical simulations. The results are formulated in classical mathematics
and proved within internal set theory which is an axiomatic approach to
nonstandard analysis.
Submitted June 1, 2009. Published January 13, 2010.
Math Subject Classifications: 34D15, 34E18, 70H09, 03H05.
Key Words: Singular perturbations; Hamiltonian system; stroboscopy lemma;
nonstandard analysis.
Show me the PDF file (405 KB),
TEX file for this article.
 |
Maamar Benbachir
Université de Béchar, BP 417
Route de Kenadsa, 08000 Béchar, Algérie
email: mbenbachir2001@yahoo.fr
|
|---|
 |
Karim Yadi
Laboratoire des Systémes Dynamiques et Applications
Université Aboubekr Belkaïd
BP 119, 13000 Tlemcen Algérie
email: yadikdz@yahoo.fr, k_yadi@mail.univ-tlemcen.dz
|
|---|
 |
Rachid Bebbouchi
Faculté de Mathématiques
Université des Sciences et de la Technologie
Houari Boumediéne, Alger Bab ezzouar, Algérie
email: rbebbouchi@hotmail.com
|
|---|
Return to the EJDE web page
 .
We study systems of reduced
problems which are Hamiltonian equations, with or without a slowly varying
parameter. Tikhonov's theorem gives approximate solutions for times of order
1. Using the stroboscopic method, we give approximations for time of order
.
We study systems of reduced
problems which are Hamiltonian equations, with or without a slowly varying
parameter. Tikhonov's theorem gives approximate solutions for times of order
1. Using the stroboscopic method, we give approximations for time of order
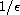 .
More precisely, the variation of the total energy of the
problem, and the eventual slow parameter, are approximated by a certain
averaged differential equation. The results are illustrated by some
numerical simulations. The results are formulated in classical mathematics
and proved within internal set theory which is an axiomatic approach to
nonstandard analysis.
.
More precisely, the variation of the total energy of the
problem, and the eventual slow parameter, are approximated by a certain
averaged differential equation. The results are illustrated by some
numerical simulations. The results are formulated in classical mathematics
and proved within internal set theory which is an axiomatic approach to
nonstandard analysis.


