Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 101, pp. 1-13.
Dependence results on almost periodic and almost automorphic
solutions of evolution equations
Joel Blot, Philippe Cieutat, Gaston M. N'Guerekata
Abstract:
We consider the semilinear evolution equations
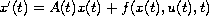 and
and
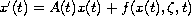 where
where
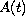 is a unbounded linear operator on a Banach space X and f
is a nonlinear operator. We study the dependence of solutions
x with respect to the function
is a unbounded linear operator on a Banach space X and f
is a nonlinear operator. We study the dependence of solutions
x with respect to the function
 in three cases: the continuous
almost periodic functions, the differentiable almost periodic
functions, and the almost automorphic functions. We give results
on the continuous dependence and on the differentiable dependence.
in three cases: the continuous
almost periodic functions, the differentiable almost periodic
functions, and the almost automorphic functions. We give results
on the continuous dependence and on the differentiable dependence.
Submitted May 25, 2010. Published July 21, 2010.
Math Subject Classifications: 47J35, 43A60, 47D06.
Key Words: Semilinear evolution equation; almost periodic function;
almost automorphic function; dependence results.
Show me the PDF file (295 KB),
TEX file for this article.
 |
Joël Blot
Laboratoire SAMM EA 4543,
Université Paris 1 Panthéon-Sorbonne
centre P.M.F., 90 rue de Tolbiac, 75634 Paris cedex 13, France
email: blot@univ-paris1.fr |
|---|
 |
Philippe Cieutat
Laboratoire de Mathématiques de Versailles, UMR-CNRS 8100
Université Versailles-Saint-Quentin-en-Yvelines
45 avenue des États-Unis, 78035 Versailles cedex, France
email: Philippe.Cieutat@math.uvsq.fr |
|---|
 |
Gaston M. N'Guérékata
Department of Mathematics
Morgan State University
1700 E. Cold Spring Lane,
Baltimore, MD 21251, USA
email: gnguerek@jewel.morgan.edu |
|---|
Return to the EJDE web page
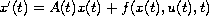 and
and
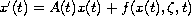 where
where
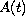 is a unbounded linear operator on a Banach space X and f
is a nonlinear operator. We study the dependence of solutions
x with respect to the function
is a unbounded linear operator on a Banach space X and f
is a nonlinear operator. We study the dependence of solutions
x with respect to the function
 in three cases: the continuous
almost periodic functions, the differentiable almost periodic
functions, and the almost automorphic functions. We give results
on the continuous dependence and on the differentiable dependence.
in three cases: the continuous
almost periodic functions, the differentiable almost periodic
functions, and the almost automorphic functions. We give results
on the continuous dependence and on the differentiable dependence.


