Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 112, pp. 1-14.
Multiple solutions for a singular semilinear elliptic problems
with critical exponent and symmetries
Alfredo Cano, Sergio Hernandez-Linares, Eric Hernandez-Martinez
Abstract:
We consider the singular semilinear elliptic equation
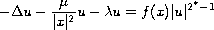
in
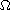 ,
,
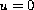 on
on
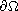 ,
where
,
where
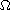 is a smooth bounded domain, in
is a smooth bounded domain, in
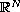 ,
,
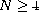 ,
,
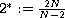 is the critical Sobolev exponent,
is the critical Sobolev exponent,
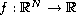 is a continuous function,
is a continuous function,
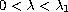 , where
, where
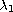 is the first
Dirichlet eigenvalue of
is the first
Dirichlet eigenvalue of
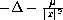 in
in
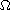 and
and
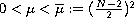 .
We show that if
.
We show that if
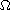 and f are invariant under a subgroup of
and f are invariant under a subgroup of
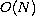 ,
the effect of the equivariant topology of
,
the effect of the equivariant topology of
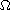 will give many symmetric nodal solutions, which extends previous results of
Guo and Niu [8].
will give many symmetric nodal solutions, which extends previous results of
Guo and Niu [8].
Submitted November 15, 2009. Published August 16, 2010.
Math Subject Classifications: 35J20, 35J25, 49J52, 58E35,74G35.
Key Words: Critical points; critical Sobolev exponent;
multiplicity of solutions; invariant under the action
of a orthogonal group; Palais-Smale condition;
singular semilinear elliptic problem; relative category.
Show me the PDF file (293 KB),
TEX file for this article.
 |
Alfredo Cano Rodríguez
Universidad Autónoma del Estado de México
Facultad de Ciencias,
Departamento de Matemáticas
Campus El Cerrillo Piedras Blancas
Carretera Toluca-Ixtlahuaca, Km 15.5, Toluca,
Estado de México, México
email: calfredo420@gmail.com
|
|---|
 |
Sergio Hernández-Linares
Universidad Autónoma Metropolitana, Cuajimalpa
Departamento de Matemáticas Aplicadas y Sistemas
Artificios No. 40, Col. Hidalgo
Del. Alvaro Obregón, C.P. 01120
México D.F., México}
email: slinares@correo.cua.uam.mx
|
|---|
 |
Eric Hernández-Martínez
Universidad Autónoma de la Ciudad de México,
Colegio de Ciencia y Tecnología.
Academia de Matemáticas,
Calle Prolongación San Isidro No. 151,
Col. San Lorenzo Tezonco, Del. Iztapalapa, C.P. 09790,
México D.F., México
email: ebric2001@hotmail.com
|
|---|
Return to the EJDE web page
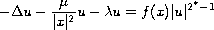
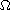 ,
,
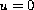 on
on
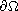 ,
where
,
where
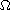 is a smooth bounded domain, in
is a smooth bounded domain, in
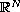 ,
,
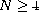 ,
,
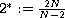 is the critical Sobolev exponent,
is the critical Sobolev exponent,
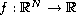 is a continuous function,
is a continuous function,
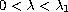 , where
, where
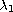 is the first
Dirichlet eigenvalue of
is the first
Dirichlet eigenvalue of
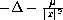 in
in
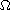 and
and
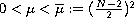 .
We show that if
.
We show that if
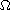 and f are invariant under a subgroup of
and f are invariant under a subgroup of
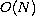 ,
the effect of the equivariant topology of
,
the effect of the equivariant topology of
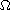 will give many symmetric nodal solutions, which extends previous results of
Guo and Niu [8].
will give many symmetric nodal solutions, which extends previous results of
Guo and Niu [8].


