Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 116, pp. 1-14.
Asymptotic behavior of ground state solution for Henon type systems
Ying Wang, Jianfu Yang
Abstract:
In this article, we investigate the asymptotic behavior of
positive ground state solutions, as
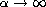 ,
for the following Henon type system
,
for the following Henon type system
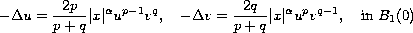
with zero boundary condition, where
 (
(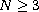 )
is the unit ball centered at the origin,
)
is the unit ball centered at the origin,
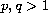 ,
,
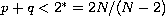 .
We show that both components of the ground solution pair
.
We show that both components of the ground solution pair
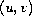 concentrate on the same point on the boundary
concentrate on the same point on the boundary
 as
as
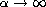 .
.
Submitted July 14, 2010. Published August 20, 2010.
Math Subject Classifications: 35J50, 35J57, 35J47.
Key Words: Asymptotic behavior; Henon systems; ground state solution
Show me the PDF file (256 KB),
TEX file for this article.
Ying Wang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: yingwang00@126.com
|
Jianfu Yang
Department of Mathematics, Jiangxi Normal University
Nanchang, Jiangxi 330022, China
email: jfyang_2000@yahoo.com
|
Return to the EJDE web page
 ,
for the following Henon type system
,
for the following Henon type system
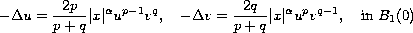
 (
(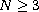 )
is the unit ball centered at the origin,
)
is the unit ball centered at the origin,
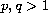 ,
,
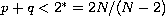 .
We show that both components of the ground solution pair
.
We show that both components of the ground solution pair
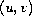 concentrate on the same point on the boundary
concentrate on the same point on the boundary
 as
as
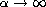 .
.