Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 131, pp. 1-11.
Oscillation of solutions for third order
functional dynamic equations
Elmetwally M. Elabbasy, Taher S. Hassan
Abstract:
In this article we study the oscillation of solutions to
the third order nonlinear functional dynamic equation
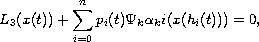
on an arbitrary time scale
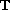 . Here
. Here
![$$
L_0(x(t))=x(t),\quad L_k(x(t))=\Big(\frac{[
L_{k-1}x(t)]^{\Delta }}{a_k(t)}\Big)^{\gamma_kk}, \quad k=1,2,3
$$](gifs/ac.gif)
with
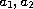 positive rd-continuous functions on
positive rd-continuous functions on
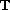 and
and
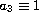 ;
the functions
;
the functions
 are nonnegative rd-continuous
on
are nonnegative rd-continuous
on
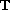 and not all
and not all
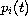 vanish in a neighborhood
of infinity;
vanish in a neighborhood
of infinity;
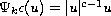 ,
,
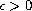 .
Our main results extend known results and are illustrated by examples.
.
Our main results extend known results and are illustrated by examples.
Submitted April 13, 2010. Published September 14, 2010.
Math Subject Classifications: 34K11, 39A10, 39A99.
Key Words: Oscillation; third order; functional dynamic equations;
time scales.
Show me the PDF file (271 KB),
TEX file for this article.
 |
Elmetwally M. Elabbasy
Department of Mathematics, Faculty of Science
Mansoura University,
Mansoura, 35516, Egypt
email: emelabbasy@mans.edu.eg
http://www.mans.edu.eg/pcvs/10805/
|
|---|
 |
Taher S. Hassan
Department of Mathematics, Faculty of Science
Mansoura University,
Mansoura, 35516, Egypt
email: tshassan@mans.edu.eg
http://www.mans.edu.eg/pcvs/10805/
|
|---|
Return to the EJDE web page
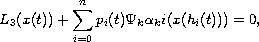
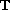 . Here
. Here
![$$
L_0(x(t))=x(t),\quad L_k(x(t))=\Big(\frac{[
L_{k-1}x(t)]^{\Delta }}{a_k(t)}\Big)^{\gamma_kk}, \quad k=1,2,3
$$](gifs/ac.gif)
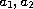 positive rd-continuous functions on
positive rd-continuous functions on
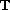 and
and
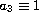 ;
the functions
;
the functions
 are nonnegative rd-continuous
on
are nonnegative rd-continuous
on
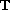 and not all
and not all
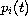 vanish in a neighborhood
of infinity;
vanish in a neighborhood
of infinity;
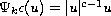 ,
,
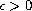 .
Our main results extend known results and are illustrated by examples.
.
Our main results extend known results and are illustrated by examples.

