Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 137, pp. 1-14.
Heteroclinic solutions to an asymptotically autonomous
second-order equation
Gregory S. Spradlin
Abstract:
We study the differential equation
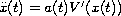 ,
where
,
where
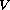 is a double-well potential with minima at
is a double-well potential with minima at
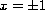 and
and
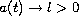 as
as
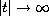 .
It is proven that under certain additional assumptions on
.
It is proven that under certain additional assumptions on
 ,
there exists a heteroclinic solution
,
there exists a heteroclinic solution
 to the differential
equation with
to the differential
equation with
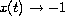 as
as
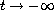 and
and
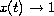 as
as
 .
The assumptions allow
.
The assumptions allow
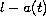 to change sign for arbitrarily large values of
to change sign for arbitrarily large values of
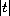 ,
and do not restrict the decay rate of
,
and do not restrict the decay rate of
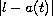 as
as
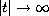 .
.
Submitted May 21, 2009. Published September 23, 2010.
Math Subject Classifications: 34B40, 34C37.
Key Words: Heteroclinic; non-autonomous equation;
bounded solution; variational methods.
Show me the PDF file (263 KB),
TEX file for this article.
 |
Gregory S. Spradlin
Department of Mathematics,
Embry-Riddle University
Daytona Beach, Florida 32114-3900, USA
email: spradlig@erau.edu
|
Return to the EJDE web page
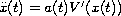 ,
where
,
where
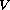 is a double-well potential with minima at
is a double-well potential with minima at
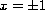 and
and
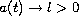 as
as
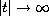 .
It is proven that under certain additional assumptions on
.
It is proven that under certain additional assumptions on
 ,
there exists a heteroclinic solution
,
there exists a heteroclinic solution
 to the differential
equation with
to the differential
equation with
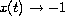 as
as
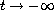 and
and
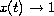 as
as
 .
The assumptions allow
.
The assumptions allow
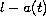 to change sign for arbitrarily large values of
to change sign for arbitrarily large values of
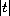 ,
and do not restrict the decay rate of
,
and do not restrict the decay rate of
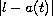 as
as
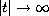 .
.
