Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 142, pp. 1-15.
Remark on well-posedness and ill-posedness for the KdV equation
Takamori Kato
Abstract:
We consider the Cauchy problem for the KdV equation with low
regularity initial data given in the space
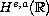 ,
which is defined by the norm
,
which is defined by the norm
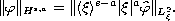
We obtain the local well-posedness in
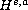 with
with
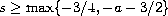 ,
,
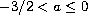 and
and
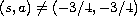 .
The proof is based on Kishimoto's work [12] which proved
the sharp well-posedness in the Sobolev space
.
The proof is based on Kishimoto's work [12] which proved
the sharp well-posedness in the Sobolev space
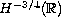 .
Moreover we prove ill-posedness when
.
Moreover we prove ill-posedness when
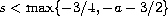 ,
,
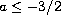 or
or
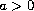 .
.
Submitted August 19, 2010. Published October 8, 2010.
Math Subject Classifications: 35Q55.
Key Words: KdV equation; well-posedness; ill-posedness; Cauchy problem;
Fourier restriction norm; low regularity.
Show me the PDF file (311 KB),
TEX file for this article.
 |
Takamori Kato
Graduate School of Mathematics, Nagoya University
Chikusa-ku, Nagoya, 464-8602, Japan
email: d08003r@math.nagoya-u.ac.jp
|
|---|
Return to the EJDE web page
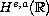 ,
which is defined by the norm
,
which is defined by the norm
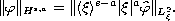
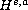 with
with
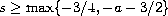 ,
,
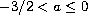 and
and
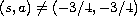 .
The proof is based on Kishimoto's work [12] which proved
the sharp well-posedness in the Sobolev space
.
The proof is based on Kishimoto's work [12] which proved
the sharp well-posedness in the Sobolev space
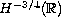 .
Moreover we prove ill-posedness when
.
Moreover we prove ill-posedness when
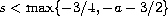 ,
,
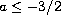 or
or
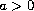 .
.
