Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 146, pp. 1-7.
Existence of non-oscillatory solutions for a
higher-order nonlinear neutral difference equation
Zhenyu Guo, Min Liu
Abstract:
This article concerns the solvability of the higher-order
nonlinear neutral delay difference equation
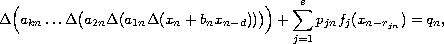
where
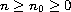 ,
,
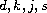 are positive integers,
are positive integers,
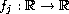 and
and
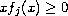 for
for
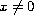 .
Sufficient conditions for the existence of non-oscillatory solutions
are established by using Krasnoselskii fixed point theorem.
Five theorems are stated according to the range of
the sequence
.
Sufficient conditions for the existence of non-oscillatory solutions
are established by using Krasnoselskii fixed point theorem.
Five theorems are stated according to the range of
the sequence
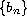 .
.
Submitted July 30, 2010. Published October 14, 2010.
Math Subject Classifications: 34K15, 34C10.
Key Words: Nonoscillatory solution; neutral difference equation;
Krasnoselskii fixed point theorem.
Show me the PDF file (231 KB),
TEX file for this article.
 |
Zhenyu Guo
School of Sciences, Liaoning Shihua University
Fushun, Liaoning 113001, China
email: guozy@163.com
|
|---|
 |
Min Liu
School of Sciences, Liaoning Shihua University
Fushun, Liaoning 113001, China
email: min_liu@yeah.net
|
|---|
Return to the EJDE web page
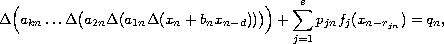
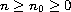 ,
,
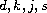 are positive integers,
are positive integers,
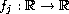 and
and
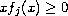 for
for
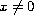 .
Sufficient conditions for the existence of non-oscillatory solutions
are established by using Krasnoselskii fixed point theorem.
Five theorems are stated according to the range of
the sequence
.
Sufficient conditions for the existence of non-oscillatory solutions
are established by using Krasnoselskii fixed point theorem.
Five theorems are stated according to the range of
the sequence
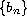 .
.

