Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 149, pp. 1-13.
Monotone iterative method for semilinear impulsive
evolution equations of mixed type in Banach spaces
Pengyu Chen, Jia Mu
Abstract:
We use a monotone iterative method in the presence of lower
and upper solutions to discuss the existence and uniqueness
of mild solutions for the initial value problem

where
 is a closed linear operator
and
is a closed linear operator
and
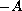 generates a strongly continuous semigroup
generates a strongly continuous semigroup
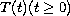 in
in
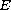 .
Under wide monotonicity conditions and the non-compactness measure
condition of the nonlinearity f, we obtain the
existence of extremal mild solutions and a unique mild solution
between lower and upper solutions requiring only that
.
Under wide monotonicity conditions and the non-compactness measure
condition of the nonlinearity f, we obtain the
existence of extremal mild solutions and a unique mild solution
between lower and upper solutions requiring only that
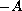 generate a strongly continuous semigroup.
generate a strongly continuous semigroup.
Submitted August 4, 2010. Published October 21, 2010.
Math Subject Classifications: 34K30, 34K45, 35F25.
Key Words: Initial value problem; lower and upper solution;
impulsive integro-differential evolution equation;
C0-semigroup; cone.
Show me the PDF file (246 KB),
TEX file for this article.
 |
Pengyu Chen
Department of Mathematics, Northwest Normal University
Lanzhou 730070, China
email: chpengyu123@163.com
|
|---|
 |
Jia Mu
Department of Mathematics, Northwest Normal University
Lanzhou 730070, China
email: mujia05@lzu.cn
|
|---|
Return to the EJDE web page

 is a closed linear operator
and
is a closed linear operator
and
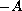 generates a strongly continuous semigroup
generates a strongly continuous semigroup
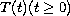 in
in
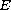 .
Under wide monotonicity conditions and the non-compactness measure
condition of the nonlinearity f, we obtain the
existence of extremal mild solutions and a unique mild solution
between lower and upper solutions requiring only that
.
Under wide monotonicity conditions and the non-compactness measure
condition of the nonlinearity f, we obtain the
existence of extremal mild solutions and a unique mild solution
between lower and upper solutions requiring only that
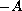 generate a strongly continuous semigroup.
generate a strongly continuous semigroup.

