Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 166, pp. 1-10.
Impulsive boundary-value problems for first-order
integro-differential equations
Xiaojing Wang, Chuanzhi Bai
Abstract:
This article concerns boundary-value problems
of first-order nonlinear impulsive integro-differential
equations:
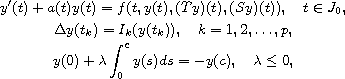
where
![$J_0 = [0, c] \setminus \{t_1, t_2, \dots , t_p\}$](gifs/ab.gif) ,
,
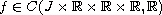 ,
,
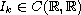 ,
,
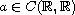 and
and
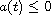 for
for
![$t \in [0, c]$](gifs/ag.gif) .
Sufficient conditions for
the existence of coupled extreme quasi-solutions are established
by using the method of lower and upper solutions and monotone
iterative technique. Wang and Zhang [18] studied the
existence of extremal solutions for a particular case of this problem,
but their solution is incorrect.
.
Sufficient conditions for
the existence of coupled extreme quasi-solutions are established
by using the method of lower and upper solutions and monotone
iterative technique. Wang and Zhang [18] studied the
existence of extremal solutions for a particular case of this problem,
but their solution is incorrect.
Submitted November 1, 2010. Published November 17, 2010.
Math Subject Classifications: 34A37, 34B15.
Key Words: Impulsive integro-differential equation;
coupled lower-upper quasi-solutions;
monotone iterative technique.
Show me the PDF file (225 KB),
TEX file for this article.
 |
Xiaojing Wang
Department of Mathematics,
Huaiyin Normal University
Huaian, Jiangsi 223300, China
email: wangxj2010106@sohu.com
|
|---|
 |
Chuanzhi Bai
Department of Mathematics,
Huaiyin Normal University
Huaian, Jiangsi 223300, China
email: czbai8@sohu.com
|
|---|
Return to the EJDE web page
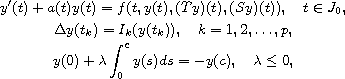
![$J_0 = [0, c] \setminus \{t_1, t_2, \dots , t_p\}$](gifs/ab.gif) ,
,
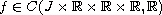 ,
,
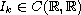 ,
,
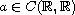 and
and
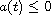 for
for
![$t \in [0, c]$](gifs/ag.gif) .
Sufficient conditions for
the existence of coupled extreme quasi-solutions are established
by using the method of lower and upper solutions and monotone
iterative technique. Wang and Zhang [18] studied the
existence of extremal solutions for a particular case of this problem,
but their solution is incorrect.
.
Sufficient conditions for
the existence of coupled extreme quasi-solutions are established
by using the method of lower and upper solutions and monotone
iterative technique. Wang and Zhang [18] studied the
existence of extremal solutions for a particular case of this problem,
but their solution is incorrect.

