Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 169, pp. 1-10.
Persistence of solutions to nonlinear evolution equations in
weighted Sobolev spaces
Xavier Carvajal Paredes, Pedro Gamboa Romero
Abstract:
In this article, we prove that the initial value problem associated with
the Korteweg-de Vries equation is well-posed in weighted
Sobolev spaces
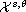 ,
for
,
for
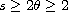 and the initial value problem
associated with the nonlinear Schrodinger equation is
well-posed in weighted Sobolev spaces
and the initial value problem
associated with the nonlinear Schrodinger equation is
well-posed in weighted Sobolev spaces
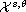 ,
for
,
for
 . Persistence property has been
proved by approximation of the solutions and using
a priori estimates.
. Persistence property has been
proved by approximation of the solutions and using
a priori estimates.
Submitted October 18, 2010. Published November 24, 2010.
Math Subject Classifications: 35A07, 35Q53.
Key Words: Schrodinger equation; Korteweg-de Vries equation;
global well-posed; persistence property; weighted Sobolev spaces.
Show me the PDF file (246 KB),
TEX file for this article.
 |
Xavier Carvajal
IM UFRJ, Av. Athos da Silveira Ramos
P.O. Box 68530. CEP 21945-970. RJ. Brazil
email: carvajal@im.ufrj.br, Phone 55-21-25627520
|
|---|
 |
Pedro Gamboa Romero
IM UFRJ, Av. Athos da Silveira Ramos
P.O. Box 68530. CEP 21945-970. RJ. Brazil
email: pgamboa@im.ufrj.br, Phone 55-21-25627520
|
|---|
Return to the EJDE web page
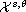 ,
for
,
for
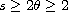 and the initial value problem
associated with the nonlinear Schrodinger equation is
well-posed in weighted Sobolev spaces
and the initial value problem
associated with the nonlinear Schrodinger equation is
well-posed in weighted Sobolev spaces
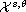 ,
for
,
for
 . Persistence property has been
proved by approximation of the solutions and using
a priori estimates.
. Persistence property has been
proved by approximation of the solutions and using
a priori estimates.

