Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 29, pp. 1-10.
Homoclinic solutions for second-order non-autonomous
Hamiltonian systems without global Ambrosetti-Rabinowitz
conditions
Rong Yuan, Ziheng Zhang
Abstract:
This article studies the existence of homoclinic solutions
for the second-order non-autonomous Hamiltonian system
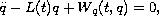
where
 is a symmetric and positive
definite matrix for all
is a symmetric and positive
definite matrix for all
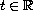 .
The function
.
The function
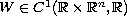 is not assumed to satisfy the global Ambrosetti-Rabinowitz
condition. Assuming reasonable conditions on
is not assumed to satisfy the global Ambrosetti-Rabinowitz
condition. Assuming reasonable conditions on
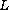 and
and
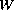 ,
we prove the existence of at least one nontrivial homoclinic solution,
and for
,
we prove the existence of at least one nontrivial homoclinic solution,
and for
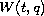 even in
even in
 , we prove the existence of infinitely
many homoclinic solutions.
, we prove the existence of infinitely
many homoclinic solutions.
Submitted January 14, 2010. Published February 25, 2010.
Math Subject Classifications: 34C37, 35A15, 37J45.
Key Words: Homoclinic solutions; critical point; variational methods;
mountain pass theorem.
Show me the PDF file (247 KB),
TEX file for this article.
 |
Rong Yuan
School of Mathematical Sciences,
Beijing Normal University
Laboratory of Mathematics and Complex Systems
Ministry of Education, Beijing 100875, China
email: ryuan@bnu.edu.cn |
|---|
 |
Ziheng Zhang
School of Mathematical Sciences,
Beijing Normal University
Laboratory of Mathematics and Complex Systems
Ministry of Education, Beijing 100875, China
email: zhzh@mail.bnu.edu.cn |
|---|
Return to the EJDE web page
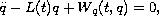
 is a symmetric and positive
definite matrix for all
is a symmetric and positive
definite matrix for all
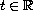 .
The function
.
The function
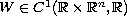 is not assumed to satisfy the global Ambrosetti-Rabinowitz
condition. Assuming reasonable conditions on
is not assumed to satisfy the global Ambrosetti-Rabinowitz
condition. Assuming reasonable conditions on
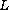 and
and
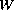 ,
we prove the existence of at least one nontrivial homoclinic solution,
and for
,
we prove the existence of at least one nontrivial homoclinic solution,
and for
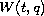 even in
even in
 , we prove the existence of infinitely
many homoclinic solutions.
, we prove the existence of infinitely
many homoclinic solutions.

