Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 76, pp. 1-9.
Solutions of a partial differential equation related to the
oplus operator
Wanchak Satsanit
Abstract:
In this article, we consider the equation
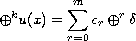
where
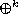 is the operator iterated k times and
defined by
is the operator iterated k times and
defined by
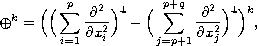
where
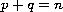 ,
,
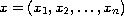 is in
the n-dimensional Euclidian space
is in
the n-dimensional Euclidian space
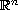 ,
,
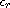 is a constant,
is a constant,
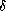 is the
Dirac-delta distribution,
is the
Dirac-delta distribution,
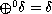 , and
, and
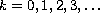 .
It is shown that, depending on the
relationship between k and m, the solution to this equation
can be ordinary functions, tempered distributions,
or singular distributions.
.
It is shown that, depending on the
relationship between k and m, the solution to this equation
can be ordinary functions, tempered distributions,
or singular distributions.
Submitted April 8, 2010. Published June 8, 2010.
Math Subject Classifications: 46F10, 46F12.
Key Words: Ultra-hyperbolic kernel; diamond operator;
tempered distribution.
Show me the PDF file (213 KB),
TEX file for this article.
 |
Wanchak Satsanit
Department of Mathematics
Faculty of Science, Maejo University
Chiang Mai, 50290 Thailand
email: aunphue@live.com
|
|---|
Return to the EJDE web page
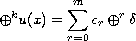
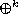 is the operator iterated k times and
defined by
is the operator iterated k times and
defined by
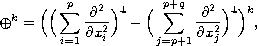
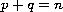 ,
,
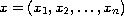 is in
the n-dimensional Euclidian space
is in
the n-dimensional Euclidian space
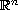 ,
,
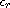 is a constant,
is a constant,
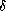 is the
Dirac-delta distribution,
is the
Dirac-delta distribution,
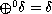 , and
, and
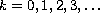 .
It is shown that, depending on the
relationship between k and m, the solution to this equation
can be ordinary functions, tempered distributions,
or singular distributions.
.
It is shown that, depending on the
relationship between k and m, the solution to this equation
can be ordinary functions, tempered distributions,
or singular distributions.
