We study the p-Laplace equation with Potentials

 ,
,
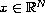 where
where
 ,
,
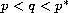 . Using a concentration-compactness principle
from critical point theory, we obtain existence,
multiplicity solutions, and concentration of solutions.
. Using a concentration-compactness principle
from critical point theory, we obtain existence,
multiplicity solutions, and concentration of solutions.
Mingzhu Wu, Zuodong Yang
Abstract:
We study the p-Laplace equation with Potentials

 ,
,
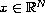 where
where
 ,
,
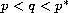 . Using a concentration-compactness principle
from critical point theory, we obtain existence,
multiplicity solutions, and concentration of solutions.
. Using a concentration-compactness principle
from critical point theory, we obtain existence,
multiplicity solutions, and concentration of solutions.
Submitted January 22, 2010. Published July 15, 2010.
Math Subject Classifications: 35J25, 35J60.
Key Words: Potentials; critical point theory; concentration;
existence; concentration-compactness; p-Laplace.
Show me the PDF file (250 KB), TEX file for this article.
| Mingzhu Wu Institute of Mathematics, School of Mathematical Science Nanjing Normal University Jiangsu Nanjing 210046, China email: wumingzhu_2010@163.com | |
 |
Zuodong Yang Institute of Mathematics, School of Mathematical Science Nanjing Normal University Jiangsu Nanjing 210046, China email: zdyang_jin@263.net |
Return to the EJDE web page