Electron. J. Diff. Equ.,
Vol. 2010(2010), No. 99, pp. 1-5.
Stability of delay differential equations with
oscillating coefficients
Michael I. Gil'
Abstract:
We study the solutions to the delay differential equation equation
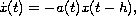
where the coefficient
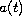 is not necessarily positive.
It is proved that this equation is exponentially stable provided
that
is not necessarily positive.
It is proved that this equation is exponentially stable provided
that
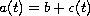 for some positive constant b less than
for some positive constant b less than
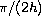 , and the integral
, and the integral
 is sufficiently
small for all
is sufficiently
small for all
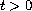 . In this case the 3/2-stability theorem
is improved.
. In this case the 3/2-stability theorem
is improved.
Submitted April 13, 2010. Published July 22, 2010.
Math Subject Classifications: 34K20.
Key Words: Linear delay differential equation; exponential stability.
Show me the PDF file (171 KB),
TEX file for this article.
 |
Michael I. Gil'
Department of Mathematics
Ben Gurion University of the Negev
P.0. Box 653, Beer-Sheva 84105, Israel
email: gilmi@cs.bgu.ac.il
|
|---|
Return to the EJDE web page
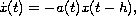
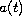 is not necessarily positive.
It is proved that this equation is exponentially stable provided
that
is not necessarily positive.
It is proved that this equation is exponentially stable provided
that
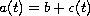 for some positive constant b less than
for some positive constant b less than
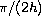 , and the integral
, and the integral
 is sufficiently
small for all
is sufficiently
small for all
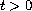 . In this case the 3/2-stability theorem
is improved.
. In this case the 3/2-stability theorem
is improved.
