Electron. J. Diff. Equ.,
Vol. 2011(2011), No. 04, pp. 1-09.
Solution to the triharmonic heat equation
Wanchak Satsanit
Abstract:
In this article, we study the equation
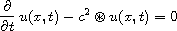
with initial condition
 . Where
x is in the Euclidean space
. Where
x is in the Euclidean space
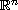 ,
,
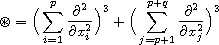
with
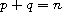 ,
,
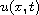 is an unknown function,
is an unknown function,
 ,
,
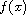 is a generalized function, and c is a positive
constant.
Under suitable conditions on f and u, we obtain a
unique solution. Note that for
is a generalized function, and c is a positive
constant.
Under suitable conditions on f and u, we obtain a
unique solution. Note that for
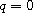 , we
have the triharmonic heat equation
, we
have the triharmonic heat equation
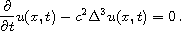
Submitted June 14, 2010. Published January 7, 2011.
Math Subject Classifications: 46F10, 46F12.
Key Words: Fourier transform; tempered distribution; diamond operator.
Show me the PDF file (211 KB),
TEX file for this article.
 |
Wanchak Satsanit
Department of Mathematics,
Faculty of Science
Maejo University,
Chiangmai, 50290, Thailand
email: aunphue@live.com
|
|---|
Return to the EJDE web page
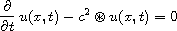
 . Where
x is in the Euclidean space
. Where
x is in the Euclidean space
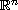 ,
,
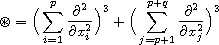
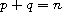 ,
,
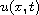 is an unknown function,
is an unknown function,
 ,
,
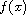 is a generalized function, and c is a positive
constant.
Under suitable conditions on f and u, we obtain a
unique solution. Note that for
is a generalized function, and c is a positive
constant.
Under suitable conditions on f and u, we obtain a
unique solution. Note that for
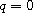 , we
have the triharmonic heat equation
, we
have the triharmonic heat equation