Electron. J. Diff. Equ., Vol. 2011 (2011), No. 11, pp. 1-8.

Existence of positive solutions for self-adjoint boundary-value problems with integral boundary conditions at resonance

Aijun Yang, Bo Sun, Weigao Ge

Abstract:
In this article, we study the self-adjoint second-order boundary-value problem with integral boundary conditions,
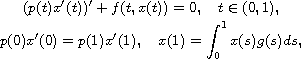
$$\displaylines{ (p(t)x'(t))'+ f(t,x(t))=0,\quad t\in (0,1),\cr p(0)x'(0)=p(1)x'(1),\quad x(1)=\int_0^1x(s)g(s)ds, }$$
which involves an integral boundary condition. We prove the existence of positive solutions using a new tool: the Leggett-Williams norm-type theorem for coincidences.

Submitted September 29, 2010. Published January 20, 2011.
Math Subject Classifications: 34B10, 34B15, 34B45.
Key Words: Boundary value problem; resonance; cone; positive solution; coincidence.

An addendum was attached on March 14, 2011. It corrects Remark 3.3, and gives credit for results quoted from [6,9].

Show me the PDF file (203 KB), TEX file, and other files for this article.

Aijun Yang
College of Science
Zhejiang University of Technology
Hangzhou, Zhejiang, 310032, China
email: yangaij2004@163.com
Bo Sun
School of Applied Mathematics
Central University of Finance and Economics
Beijing, 100081, China
email: sunbo19830328@163.com
Weigao Ge
Department of Applied Mathematics
Beijing Institute of Technology
Beijing, 100081, China
email: gew@bit.edu.cn

Return to the EJDE web page