Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 19, pp. 1-21.
Quadratic forms as Lyapunov functions in the study of stability
of solutions to difference equations
Alexander O. Ignatyev, Oleksiy Ignatyev
Abstract:
A system of linear autonomous difference equations
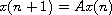 is considered, where
is considered, where
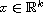 ,
,
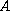 is a real nonsingular
is a real nonsingular
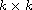 matrix.
In this paper it has been proved that if
matrix.
In this paper it has been proved that if
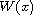 is any quadratic
form and
is any quadratic
form and
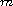 is any positive integer, then there exists a unique
quadratic form
is any positive integer, then there exists a unique
quadratic form
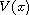 such that
such that
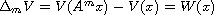 holds if and only if
holds if and only if
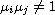 (
(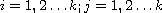 )
where
)
where
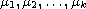 are the roots of the equation
are the roots of the equation
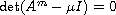 .
.
A number of theorems on the stability of difference systems have
also been proved. Applying these theorems, the stability problem
of the zero solution of the nonlinear system
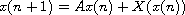 has been solved in the critical case when one eigenvalue of
a matrix
has been solved in the critical case when one eigenvalue of
a matrix
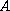 is equal to minus one, and others lie inside the
unit disk of the complex plane.
is equal to minus one, and others lie inside the
unit disk of the complex plane.
Submitted February 1, 2010. Published February 3, 2011.
Math Subject Classifications: 39A11, 34K20.
Key Words: Difference equations; Lyapunov function.
Show me the PDF file (353 KB),
TEX file for this article.
 |
Alexander O. Ignatyev
Institute for Applied Mathematics and Mechanics
R. Luxemburg Street,74, Donetsk-83114, Ukraine
email: aoignat@mail.ru, ignat@iamm.ac.donetsk.ua
|
|---|
 |
Oleksiy Ignatyev
Department of Statistics and Probability
Michigan State University
A408 Wells Hall, East Lansing, MI 48824-1027, USA
email: ignatyev@stt.msu.edu, aignatye@math.kent.edu
|
|---|
Return to the EJDE web page
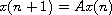 is considered, where
is considered, where
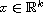 ,
,
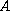 is a real nonsingular
is a real nonsingular
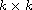 matrix.
In this paper it has been proved that if
matrix.
In this paper it has been proved that if
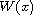 is any quadratic
form and
is any quadratic
form and
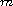 is any positive integer, then there exists a unique
quadratic form
is any positive integer, then there exists a unique
quadratic form
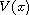 such that
such that
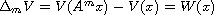 holds if and only if
holds if and only if
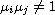 (
(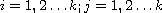 )
where
)
where
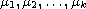 are the roots of the equation
are the roots of the equation
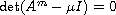 .
.
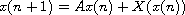 has been solved in the critical case when one eigenvalue of
a matrix
has been solved in the critical case when one eigenvalue of
a matrix
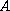 is equal to minus one, and others lie inside the
unit disk of the complex plane.
is equal to minus one, and others lie inside the
unit disk of the complex plane.

