Electron. J. Diff. Equ.,
Vol. 2011 (2011), No. 30, pp. 1-12.
Existence of infinitely many solutions for degenerate and
singular elliptic systems with indefinite concave nonlinearities
Nguyen Thanh Chung
Abstract:
In this article, we consider degenerate and singular
elliptic systems of the form
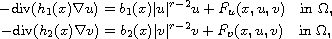
where
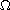 is a bounded domain in
is a bounded domain in
 ,
,
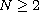 ,
with smooth boundary
,
with smooth boundary
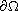 ;
;
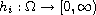 ,
,
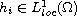 ,
and are allowed to have "essential" zeroes;
,
and are allowed to have "essential" zeroes;
 ;
the weight functions
;
the weight functions
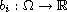 ,
may be sign-changing; and
,
may be sign-changing; and
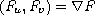 .
Using variational techniques, a variant of the
Caffarelli - Kohn - Nirenberg inequality, and a variational
principle by Clark [9], we prove the rxistence of
infinitely many solutions in a weighted Sobolev space.
.
Using variational techniques, a variant of the
Caffarelli - Kohn - Nirenberg inequality, and a variational
principle by Clark [9], we prove the rxistence of
infinitely many solutions in a weighted Sobolev space.
Submitted May 14, 2010. Published February 18, 2011.
Math Subject Classifications: 35J65, 35J20.
Key Words: Degenerate and singular Elliptic system; weight function;
concave nonlinearity; infinitely many solutions.
Show me the PDF file (266 KB),
TEX file for this article.
 |
Nguyen Thanh Chung
Department of Mathematics and Informatics
Quang Binh University, 312 Ly Thuong Kiet
Dong Hoi, Quang Binh, Vietnam
email: ntchung82@yahoo.com
|
|---|
Return to the EJDE web page
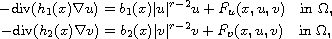
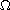 is a bounded domain in
is a bounded domain in
 ,
,
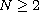 ,
with smooth boundary
,
with smooth boundary
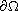 ;
;
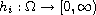 ,
,
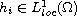 ,
and are allowed to have "essential" zeroes;
,
and are allowed to have "essential" zeroes;
 ;
the weight functions
;
the weight functions
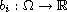 ,
may be sign-changing; and
,
may be sign-changing; and
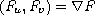 .
Using variational techniques, a variant of the
Caffarelli - Kohn - Nirenberg inequality, and a variational
principle by Clark [9], we prove the rxistence of
infinitely many solutions in a weighted Sobolev space.
.
Using variational techniques, a variant of the
Caffarelli - Kohn - Nirenberg inequality, and a variational
principle by Clark [9], we prove the rxistence of
infinitely many solutions in a weighted Sobolev space.
