Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 111, pp. 1-16.
Multiplicity of positive solutions for quasilinear elliptic
p-Laplacian systems
Asadollah Aghajani, Jamileh Shamshiri
Abstract:
We study the existence and multiplicity of solutions to
the elliptic system

where
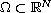 is
a bounded and smooth domain.
Using fibering maps and extracting Palais-Smale sequences in the
Nehari manifold, we prove the existence of at least two
distinct nontrivial nonnegative solutions.
is
a bounded and smooth domain.
Using fibering maps and extracting Palais-Smale sequences in the
Nehari manifold, we prove the existence of at least two
distinct nontrivial nonnegative solutions.
Submitted June 19, 2012. Published July 2, 2012.
Math Subject Classifications: 35B38, 34B15, 35J92.
Key Words: Critical points; nonlinear boundary value problems;
quasilinear p-Laplacian problem; fibering map; Nehari manifold.
Show me the PDF file (294 KB),
TEX file for this article.
 |
Asadollah Aghajani
School of Mathematics
Iran University of Science and Technology
P.O. Box 16846-13114, Narmak, Tehran, Iran
email: aghajani@iust.ac.ir
|
|---|
 |
Jamileh Shamshiri
Department of Mathematics, Karaj Branch
Islamic Azad University, Karaj, Iran
email: jamileshamshiri@gmail.com
|
|---|
Return to the EJDE web page

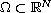 is
a bounded and smooth domain.
Using fibering maps and extracting Palais-Smale sequences in the
Nehari manifold, we prove the existence of at least two
distinct nontrivial nonnegative solutions.
is
a bounded and smooth domain.
Using fibering maps and extracting Palais-Smale sequences in the
Nehari manifold, we prove the existence of at least two
distinct nontrivial nonnegative solutions.

