Electron. J. Diff. Equ., Vol. 2012 (2012), No. 126, pp. 1-8.

Existence of positive solutions to three-point $\phi$-Laplacian BVPs via homotopic deformations

Nadir Benkaci, Abdelhamid Benmezai, Johnny Henderson

Abstract:
Under suitable conditions and via homotopic deformation, we provide existence results for a positive solution to the three-point $\phi$-Laplacian boundary-value problem
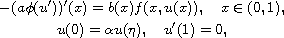
$$\displaylines{ -( a\phi(u'))'(x)=b(x) f(x,u(x)),\quad x\in ( 0,1), \cr u(0)=\alpha u(\eta),\quad u'(1)=0, }$$
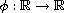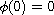where $\phi:\mathbb{R}\to\mathbb{R}$ is an increasing homeomorphism with $\phi(0) =0$, b does not vanish identically, and f is continuous.

Submitted March 12, 2012. Published August 14, 2012.
Math Subject Classifications: 34B15, 34B18.
Key Words: phi-Laplacian BVP; positive solution; fixed point; index theory.

Show me the PDF file (207 KB), TEX file, and other files for this article.

  Nadir Ali Benkaci
Faculty of Sciences, University M'Hmed Bouguerra
Boumerdes, Algeria
email: radians_2005@yahoo.fr
Abdelhamid Benmezai
Dynamical Systems Laboratory
Faculty of Mathematics, USTHB P.O. Box 32
El-Alia Bab-ezouar, Algiers, Algeria
email: abenmezai@yahoo.fr
Johnny Henderson
Department of Mathematics, Baylor University
Waco, Texas 76798-7328, USA
email: Johnny_Henderson@baylor.edu

Return to the EJDE web page