Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 159, pp. 1-6.
Dirichlet-to-Neumann operator on the perturbed unit disk
Hassan Emamirad, Mohamed-Reza Mokhtarzadeh
Abstract:
This article concerns the Laplacian on a perturbed unit
disk
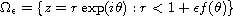 ,
with dynamical boundary condition whose solution can be represented
by a Dirichlet-to-Neumann semigroup. By neglecting the terms of order
,
with dynamical boundary condition whose solution can be represented
by a Dirichlet-to-Neumann semigroup. By neglecting the terms of order
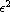 , we obtain a simple expression which allows us to use
the Chernoff's theorem for its approximation. As a motivation for
this research, we present an example which shows the feasibility of applying
of Chernoff's Theorem.
, we obtain a simple expression which allows us to use
the Chernoff's theorem for its approximation. As a motivation for
this research, we present an example which shows the feasibility of applying
of Chernoff's Theorem.
Submitted June 19, 2012. Published September 18, 2012.
Math Subject Classifications: 35J25, 47F05, 47D06.
Key Words: Dirichlet-to-Neumann operator, gamma-harmonic lifting.
Show me the PDF file (201 KB),
TEX file for this article.
 |
Hassan Emamirad
School of Mathematics
Institute for Research in Fundamental Sciences (IPM)
P.O. Box 19395-5746, Tehran, Iran
email: emamirad@ipm.ir
|
|---|
 |
Mohamed-Reza Mokhtarzadeh
School of Mathematics
Institute for Research in Fundamental Sciences (IPM)
P.O. Box 19395-5746, Tehran, Iran
email: mrmokhtarzadeh@ipm.ir
|
|---|
Return to the EJDE web page
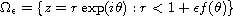 ,
with dynamical boundary condition whose solution can be represented
by a Dirichlet-to-Neumann semigroup. By neglecting the terms of order
,
with dynamical boundary condition whose solution can be represented
by a Dirichlet-to-Neumann semigroup. By neglecting the terms of order
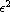 , we obtain a simple expression which allows us to use
the Chernoff's theorem for its approximation. As a motivation for
this research, we present an example which shows the feasibility of applying
of Chernoff's Theorem.
, we obtain a simple expression which allows us to use
the Chernoff's theorem for its approximation. As a motivation for
this research, we present an example which shows the feasibility of applying
of Chernoff's Theorem.

