Let
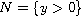 and
and
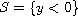 be the semi-planes of
be the semi-planes of
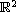 having as common boundary the line
having as common boundary the line
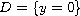 .
Let X and Y be
polynomial vector fields defined in N and
.
Let X and Y be
polynomial vector fields defined in N and
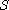 ,
respectively,
leading to a discontinuous piecewise
polynomial vector field Z=(X,Y). This work pursues the
stability and the transition analysis of solutions of Z between
N and S, started by Filippov (1988) and Kozlova (1984) and
reformulated by Sotomayor-Teixeira (1995) in terms of the
regularization method. This method consists in analyzing a one
parameter family of continuous vector fields
,
respectively,
leading to a discontinuous piecewise
polynomial vector field Z=(X,Y). This work pursues the
stability and the transition analysis of solutions of Z between
N and S, started by Filippov (1988) and Kozlova (1984) and
reformulated by Sotomayor-Teixeira (1995) in terms of the
regularization method. This method consists in analyzing a one
parameter family of continuous vector fields
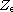 ,
defined by averaging X and Y. This family approaches Z when
the parameter goes to zero. The results of Sotomayor-Teixeira and
Sotomayor-Machado (2002) providing conditions on (X,Y) for the
regularized vector fields to be structurally stable on planar
compact connected regions are extended to discontinuous piecewise
polynomial vector fields on
,
defined by averaging X and Y. This family approaches Z when
the parameter goes to zero. The results of Sotomayor-Teixeira and
Sotomayor-Machado (2002) providing conditions on (X,Y) for the
regularized vector fields to be structurally stable on planar
compact connected regions are extended to discontinuous piecewise
polynomial vector fields on
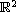 .
Pertinent genericity
results for vector fields satisfying the above stability
conditions are also extended to the present case. A procedure for
the study of discontinuous piecewise vector fields at infinity
through a compactification is proposed here.
.
Pertinent genericity
results for vector fields satisfying the above stability
conditions are also extended to the present case. A procedure for
the study of discontinuous piecewise vector fields at infinity
through a compactification is proposed here.

