Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 171, pp. 1-18.
Existence of solutions to boundary-value problems governed
by general non-autonomous nonlinear differential operators
Cristina Marcelli
Abstract:
This article concerns the existence and non-existence of solutions to
the strongly nonlinear non-autonomous boundary-value problem

with
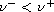 ,
where
,
where
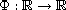 is a general
increasing homeomorphism, with
is a general
increasing homeomorphism, with
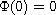 ,
a is a positive,
continuous function and f is a Caratheodory nonlinear function.
We provide sufficient conditions for the solvability which result
to be optimal for a wide class of problems. In particular,
we focus on the role played by the behaviors of
,
a is a positive,
continuous function and f is a Caratheodory nonlinear function.
We provide sufficient conditions for the solvability which result
to be optimal for a wide class of problems. In particular,
we focus on the role played by the behaviors of
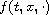 and
and
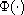 as
as
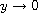 related to that of
related to that of
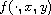 and
and
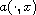 as
as
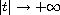 .
.
Submitted September 3, 2012. Published October 4, 2012.
Math Subject Classifications: 34B40, 34C37, 34B15, 34L30.
Key Words: Boundary value problems; unbounded domains;
heteroclinic solutions; nonlinear differential operators;
p-Laplacian operator; Phi-Laplacian operator
Show me the PDF file (331 KB),
TEX file for this article.
 |
Cristina Marcelli
Dipartimento di Scienze Matematiche
Università Politecnica delle Marche
Via Brecce Bianche, 60131 Ancona, Italy
email: marcelli@dipmat.univpm.it
|
|---|
Return to the EJDE web page

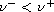 ,
where
,
where
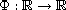 is a general
increasing homeomorphism, with
is a general
increasing homeomorphism, with
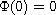 ,
a is a positive,
continuous function and f is a Caratheodory nonlinear function.
We provide sufficient conditions for the solvability which result
to be optimal for a wide class of problems. In particular,
we focus on the role played by the behaviors of
,
a is a positive,
continuous function and f is a Caratheodory nonlinear function.
We provide sufficient conditions for the solvability which result
to be optimal for a wide class of problems. In particular,
we focus on the role played by the behaviors of
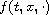 and
and
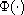 as
as
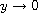 related to that of
related to that of
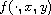 and
and
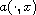 as
as
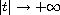 .
.
