Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 18, pp. 1-20.
Existence of a minimizer for the quasi-relativistic Kohn-Sham model
Carlos Argaez, Michael Melgaard
Abstract:
We study the standard and extended Kohn-Sham models for
quasi-relativistic N-electron Coulomb systems; that is,
systems where the kinetic energy of the electrons is given
by the quasi-relativistic operator

For spin-unpolarized systems in the local density approximation,
we prove existence of a ground state (or minimizer) provided that
the total charge
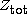 of K nuclei is greater than
N-1 and that
of K nuclei is greater than
N-1 and that
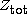 is smaller than a critical
charge
is smaller than a critical
charge
 .
.
Submitted April 12, 2011. Published January 30, 2012.
Math Subject Classifications: 35J60, 47J10, 58Z05, 81V55.
Key Words: Kohn-Sham equations; ground state; variational methods;
concentration-compactness; density operators.
Show me the PDF file (323 KB),
TEX file for this article.
 |
Carlos Argaez
School of Mathematical Sciences
Dublin Institute of Technology
Dublin 8, Ireland
|
|---|
 |
Michael Melgaard
School of Mathematical Sciences
Dublin Institute of Technology
Dublin 8, Ireland
email: mmelgaard@dit.ie
|
|---|
Return to the EJDE web page

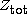 of K nuclei is greater than
N-1 and that
of K nuclei is greater than
N-1 and that
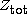 is smaller than a critical
charge
is smaller than a critical
charge
 .
.

