Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 190, pp. 1-7.
Weak compactness of biharmonic maps
Shenzhou Zheng
Abstract:
This article shows that if a sequence of weak solutions of a perturbed
biharmonic map satisfies
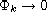 in
in
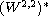 and
and
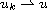 weakly in
weakly in
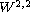 , then
, then
 is a biharmonic map.
In particular, we show that the space of biharmonic maps is sequentially
compact under the weak-
is a biharmonic map.
In particular, we show that the space of biharmonic maps is sequentially
compact under the weak-
 topology.
topology.
Submitted July 15,2012. Published October 31, 2012.
Math Subject Classifications: 35J48, 35G50, 58J05.
Key Words: Biharmonic maps, conservation law, weak compactness.
Show me the PDF file (222 KB),
TEX file for this article.
Shenzhou Zheng
Department of Mathematics
Beijing Jiaotong University
Beijing 100044, China
email: shzhzheng@bjtu.edu.cn, Tel: +1-859-257-4802
|
Return to the EJDE web page
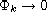 in
in
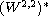 and
and
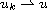 weakly in
weakly in
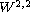 , then
, then
 is a biharmonic map.
In particular, we show that the space of biharmonic maps is sequentially
compact under the weak-
is a biharmonic map.
In particular, we show that the space of biharmonic maps is sequentially
compact under the weak-
 topology.
topology.