Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 196, pp. 1-11.
Stability of solutions for some inverse problems
Robert Dalmasso
Abstract:
In this article we establish three stability
results for some inverse problems.
More precisely we consider the following boundary value problem:
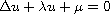 in
in
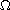 ,
,
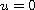 on
on
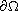 ,
where
,
where
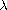 and
and
 are real constants and
are real constants and
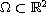 is
a smooth bounded simply-connected open set. The inverse problem consists in
the identification of
is
a smooth bounded simply-connected open set. The inverse problem consists in
the identification of
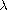 and
and
 from knowledge of the normal flux
from knowledge of the normal flux
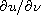 on
on
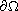 corresponding to some
nontrivial solution.
corresponding to some
nontrivial solution.
Submitted September 10, 2012. Published November 8, 2012.
Math Subject Classifications: 35J05, 35R30.
Key Words: Inverse problem; stability
Show me the PDF file (215 KB),
TEX file for this article.
 |
Robert Dalmasso
L'Eden,17 Boulevard Maurice Maeterlinck
06300 Nice, France
email: robert.dalmasso@imag.fr
|
|---|
Return to the EJDE web page
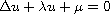 in
in
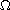 ,
,
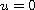 on
on
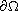 ,
where
,
where
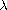 and
and
 are real constants and
are real constants and
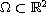 is
a smooth bounded simply-connected open set. The inverse problem consists in
the identification of
is
a smooth bounded simply-connected open set. The inverse problem consists in
the identification of
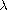 and
and
 from knowledge of the normal flux
from knowledge of the normal flux
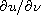 on
on
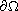 corresponding to some
nontrivial solution.
corresponding to some
nontrivial solution.
