Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 203, pp. 1-18.
Existence and upper semi-continuity of uniform attractors for
non-autonomous reaction diffusion equations on R^N
Tang Quoc Bao
Abstract:
We prove the existence of uniform attractors for the non-autonomous
reaction diffusion equation
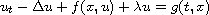
on
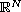 , where the external force g is translation bounded
and the nonlinearity f satisfies a polynomial growth condition.
Also, we prove the upper semi-continuity of uniform attractors
with respect to the nonlinearity.
, where the external force g is translation bounded
and the nonlinearity f satisfies a polynomial growth condition.
Also, we prove the upper semi-continuity of uniform attractors
with respect to the nonlinearity.
Submitted April 10, 2012. Published November 24, 2012.
Math Subject Classifications: 34D45, 35B41, 35K57, 35B30.
Key Words: Uniform attractors; reaction diffusion equations;
unbounded domain; upper semicontinuity.
Show me the PDF file (317 KB),
TEX file for this article.
 |
Tang Quoc Bao
School of Applied Mathematics and Informatics
Ha Noi University of Science and Technology
1 Dai Co Viet, Hai Ba Trung, Hanoi, Vietnam
email: baotangquoc@gmail.com
|
|---|
Return to the EJDE web page
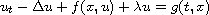
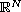 , where the external force g is translation bounded
and the nonlinearity f satisfies a polynomial growth condition.
Also, we prove the upper semi-continuity of uniform attractors
with respect to the nonlinearity.
, where the external force g is translation bounded
and the nonlinearity f satisfies a polynomial growth condition.
Also, we prove the upper semi-continuity of uniform attractors
with respect to the nonlinearity.
