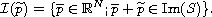Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 209, pp. 1-13.
Range of semilinear operators for systems at resonance
Pablo Amster, Mariel Paula Kuna
Abstract:
For a vector function
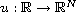 we consider the system
we consider the system
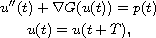
where
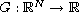 is a
is a
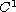 function.
We are interested in finding all possible T-periodic forcing terms
p(t) for which there is at least one solution.
In other words, we examine the
range of the semilinear operator
function.
We are interested in finding all possible T-periodic forcing terms
p(t) for which there is at least one solution.
In other words, we examine the
range of the semilinear operator
![$S:H^2_{per}\to L^2([0,T],\mathbb{R}^N)$](gifs/ae.gif) given by
given by
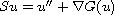 ,
where
,
where
![$$
H^2_{per}= \{ u\in H^2([0,T], \mathbb{R}^N);
u(0) - u(T) = u'(0)-u'(T)=0 \}.
$$](gifs/ag.gif)
Writing
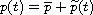 ,
where
,
where
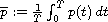 ,
we present several results concerning the topological structure of the set
,
we present several results concerning the topological structure of the set
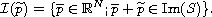
Submitted October 7, 2011. Published November 27, 2012.
Math Subject Classifications: 34B15, 34L30.
Key Words: Resonant systems; semilinear operators; critical point theory.
Show me the PDF file (269 KB),
TEX file for this article.
 |
Pablo Amster
Departamento de Matemática
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Ciudad Universitaria, Pabellón I
(1428) Buenos Aires, Argentina
email: pamster@dm.uba.ar
|
|---|
 |
Mariel Paula Kuna
Departamento de Matemática
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Ciudad Universitaria, Pabellón I
(1428) Buenos Aires, Argentina
email: mpkuna@dm.uba.ar
|
|---|
Return to the EJDE web page
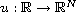 we consider the system
we consider the system
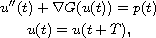
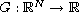 is a
is a
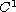 function.
We are interested in finding all possible T-periodic forcing terms
p(t) for which there is at least one solution.
In other words, we examine the
range of the semilinear operator
function.
We are interested in finding all possible T-periodic forcing terms
p(t) for which there is at least one solution.
In other words, we examine the
range of the semilinear operator
![$S:H^2_{per}\to L^2([0,T],\mathbb{R}^N)$](gifs/ae.gif) given by
given by
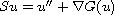 ,
where
,
where
![$$
H^2_{per}= \{ u\in H^2([0,T], \mathbb{R}^N);
u(0) - u(T) = u'(0)-u'(T)=0 \}.
$$](gifs/ag.gif)
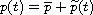 ,
where
,
where
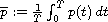 ,
we present several results concerning the topological structure of the set
,
we present several results concerning the topological structure of the set