Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 213, pp. 1-14.
Positive solutions to boundary-value problems of p-Laplacian
fractional differential equations with a parameter in the boundary
Zhenlai Han, Hongling Lu, Shurong Sun, Dianwu Yang
Abstract:
In this article, we consider the following boundary-value problem
of nonlinear fractional differential equation with
 -Laplacian operator
-Laplacian operator
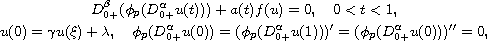
where
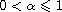 ,
,
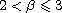 are real numbers,
are real numbers,
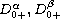 are the standard Caputo fractional derivatives,
are the standard Caputo fractional derivatives,
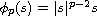 ,
,
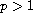 ,
,
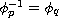 ,
,
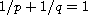 ,
,
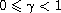 ,
,
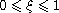 ,
,
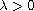 is a parameter,
is a parameter,
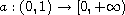 and
and
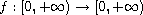 are continuous.
By the properties of Green function and Schauder fixed point theorem,
several existence and nonexistence results for positive solutions,
in terms of the parameter
are continuous.
By the properties of Green function and Schauder fixed point theorem,
several existence and nonexistence results for positive solutions,
in terms of the parameter
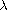 are obtained.
The uniqueness of positive solution on the parameter
are obtained.
The uniqueness of positive solution on the parameter
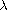 is also studied.
Some examples are presented to illustrate the main results.
is also studied.
Some examples are presented to illustrate the main results.
Submitted September 5, 2012. Published November 27, 2012.
Math Subject Classifications: 34A08, 34B18, 35J05.
Key Words: Fractional boundary-value problem; positive solution; cone;
Schauder fixed point theorem; uniqueness; p-Laplacian operator.
Show me the PDF file (272 KB),
TEX file for this article.
 |
Zhenlai Han
School of Mathematical Sciences
University of Jinan
Jinan, Shandong 250022, China
email: hanzhenlai@163.com
|
|---|
 |
Hongling Lu
School of Mathematical Sciences
University of Jinan
Jinan, Shandong 250022, China
email: lhl4578@126.com
|
|---|
 |
Shurong Sun
School of Mathematical Sciences
University of Jinan
Jinan, Shandong 250022, China
email: sshrong@163.com
|
|---|
 |
Dianwu Yang
School of Mathematical Sciences
University of Jinan
Jinan, Shandong 250022, China
email: ss_yangdw@ujn.edu.cn
|
|---|
Return to the EJDE web page
 -Laplacian operator
-Laplacian operator
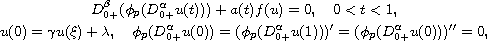
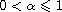 ,
,
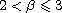 are real numbers,
are real numbers,
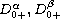 are the standard Caputo fractional derivatives,
are the standard Caputo fractional derivatives,
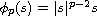 ,
,
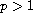 ,
,
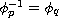 ,
,
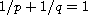 ,
,
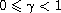 ,
,
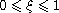 ,
,
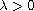 is a parameter,
is a parameter,
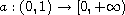 and
and
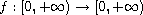 are continuous.
By the properties of Green function and Schauder fixed point theorem,
several existence and nonexistence results for positive solutions,
in terms of the parameter
are continuous.
By the properties of Green function and Schauder fixed point theorem,
several existence and nonexistence results for positive solutions,
in terms of the parameter
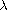 are obtained.
The uniqueness of positive solution on the parameter
are obtained.
The uniqueness of positive solution on the parameter
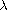 is also studied.
Some examples are presented to illustrate the main results.
is also studied.
Some examples are presented to illustrate the main results.



