Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 217, pp. 1-18.
Nodal solutions for sixth-order m-point boundary-value
problems using bifurcation methods
Yude Ji, Yanping Guo, Yukun Yao, Yingjie Feng
Abstract:
We consider the sixth-order
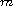 -point
boundary-value problem
-point
boundary-value problem
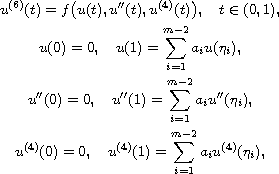
where
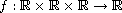 is
a sign-changing continuous function,
is
a sign-changing continuous function,
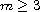 ,
,
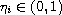 ,
and
,
and
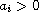 for
for
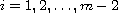 with
with
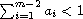 .
We first show that the spectral
properties of the linearisation of this problem are similar to the
well-known properties of the standard Sturm-Liouville problem with
separated boundary conditions. These spectral properties are then
used to prove a Rabinowitz-type global bifurcation theorem for a
bifurcation problem related to the above problem. Finally, we obtain
the existence of nodal solutions for the problem, under various
conditions on the asymptotic behaviour of nonlinearity
.
We first show that the spectral
properties of the linearisation of this problem are similar to the
well-known properties of the standard Sturm-Liouville problem with
separated boundary conditions. These spectral properties are then
used to prove a Rabinowitz-type global bifurcation theorem for a
bifurcation problem related to the above problem. Finally, we obtain
the existence of nodal solutions for the problem, under various
conditions on the asymptotic behaviour of nonlinearity
 by using
the global bifurcation theorem.
by using
the global bifurcation theorem.
Submitted June 20, 2012. Published November 29, 2012.
Math Subject Classifications: 34B15.
Key Words: Nonlinear boundary value problems; nodal solution;
eigenvalues; bifurcation methods.
Show me the PDF file (315 KB),
TEX file for this article.
 |
Yude Ji
Hebei University of Science and Technology
Shijiazhuang, 050018, Hebei, China
email: jiyude-1980@163.com
|
|---|
 |
Yanping Guo
Hebei University of Science and Technology
Shijiazhuang, 050018, Hebei, China
email: guoyanping65@sohu.com
|
|---|
 |
Yukun Yao
Hebei Medical University
Shijiazhuang, 050200, Hebei, China
email: yaoyukun126@126.com
|
|---|
 |
Yingjie Feng
Hebei Vocational Technical College of Chemical and
Medicine
Shijiazhuang, 050026, Hebei, China
email: fengyingjie126@126.com
|
|---|
Return to the EJDE web page
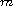 -point
boundary-value problem
-point
boundary-value problem
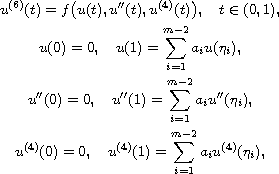
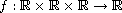 is
a sign-changing continuous function,
is
a sign-changing continuous function,
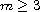 ,
,
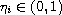 ,
and
,
and
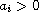 for
for
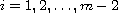 with
with
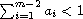 .
We first show that the spectral
properties of the linearisation of this problem are similar to the
well-known properties of the standard Sturm-Liouville problem with
separated boundary conditions. These spectral properties are then
used to prove a Rabinowitz-type global bifurcation theorem for a
bifurcation problem related to the above problem. Finally, we obtain
the existence of nodal solutions for the problem, under various
conditions on the asymptotic behaviour of nonlinearity
.
We first show that the spectral
properties of the linearisation of this problem are similar to the
well-known properties of the standard Sturm-Liouville problem with
separated boundary conditions. These spectral properties are then
used to prove a Rabinowitz-type global bifurcation theorem for a
bifurcation problem related to the above problem. Finally, we obtain
the existence of nodal solutions for the problem, under various
conditions on the asymptotic behaviour of nonlinearity
 by using
the global bifurcation theorem.
by using
the global bifurcation theorem.



