Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 218, pp. 1-10.
Weak Rolewicz's theorem in Hilbert spaces
Constantin Buse, Gul Rahmat
Abstract:
Let
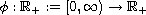 be a nondecreasing
function which is positive on
be a nondecreasing
function which is positive on
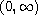 and let
and let
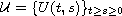 be a positive strongly continuous
periodic evolution family of bounded linear operators acting on a
complex Hilbert space
be a positive strongly continuous
periodic evolution family of bounded linear operators acting on a
complex Hilbert space
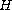 . We prove that
. We prove that
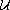 is uniformly
exponentially stable if for each unit vector
is uniformly
exponentially stable if for each unit vector
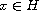 ,
one has
,
one has

The result seems to be new and it generalizes others of the same topic.
Moreover, the proof is surprisingly simple.
Submitted October 3, 2012. Published November 29, 2012.
Math Subject Classifications: 47A30, 46A30.
Key Words: Uniform exponential stability; Rolewicz's type theorems;
weak integral stability boundedness.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Constantin Buse
West University of Timisoara
Department of Mathematics
Bd. V. Parvan No. 4, 300223-Timisoara, Romania
email: buse@math.uvt.ro
|
|---|
 |
Gul Rahmat
Government College University
Abdus Salam School of Mathematical Sciences
Lahore, Pakistan
email: gulassms@gmail.com
|
|---|
Return to the EJDE web page
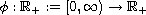 be a nondecreasing
function which is positive on
be a nondecreasing
function which is positive on
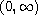 and let
and let
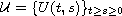 be a positive strongly continuous
periodic evolution family of bounded linear operators acting on a
complex Hilbert space
be a positive strongly continuous
periodic evolution family of bounded linear operators acting on a
complex Hilbert space
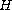 . We prove that
. We prove that
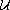 is uniformly
exponentially stable if for each unit vector
is uniformly
exponentially stable if for each unit vector
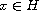 ,
one has
,
one has


