In this article, we consider the problem

where
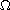 is a bounded domain in
is a bounded domain in
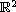 ,
,
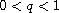 ,
and
,
and
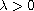 .
We show that there exists a real number
.
We show that there exists a real number
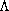 such that the above problem admits at least two solutions for
such that the above problem admits at least two solutions for
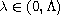 ,
and no solution for
,
and no solution for
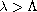 .
.
Nasreddine Megrez, K. Sreenadh, Brahim Khaldi
Abstract:
In this article, we consider the problem

where
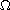 is a bounded domain in
is a bounded domain in
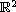 ,
,
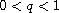 ,
and
,
and
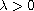 .
We show that there exists a real number
.
We show that there exists a real number
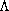 such that the above problem admits at least two solutions for
such that the above problem admits at least two solutions for
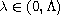 ,
and no solution for
,
and no solution for
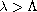 .
.
Submitted June 16, 2011. Published December 26, 2012.
Math Subject Classifications: 35J50, 35J57, 35J60.
Key Words: Gradient system; exponential nonlinearity; multiplicity.
Show me the PDF file (282 KB), TEX file for this article.
 |
Nasreddine Megrez Chemical and Material Engineering Department University of Alberta 9107 - 116 Street, Edmonton (Alberta) T6G 2V4, Canada email: nmegrez@gmail.com |
|---|---|
| K. Sreenadh Department of Mathematics Indian Institute of Technology Delhi Hauz Khaz New Delhi-16, India email: sreenadh@gmail.com | |
 |
Brahim Khaldi Departement of Sciences, University of Bechar PB 117, Bechar 08000, Algeria email: khaldibra@yahoo.fr |
Return to the EJDE web page