Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 25, pp. 1-12.
Existence of solutions for discontinuous p(x)-Laplacian problems
with critical exponents
Xudong Shang, Zhigang Wang
Abstract:
In this article, we study the existence of solutions to
the problem
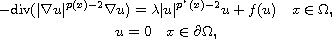
where
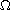 is a smooth bounded domain in
is a smooth bounded domain in
 ,
,
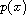 is a continuous function with
is a continuous function with
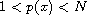 and
and
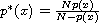 .
Applying nonsmooth critical point theory for locally Lipschitz functionals,
we show that there is at least one nontrivial solution when
.
Applying nonsmooth critical point theory for locally Lipschitz functionals,
we show that there is at least one nontrivial solution when
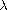 less than a certain number, and
less than a certain number, and
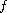 maybe discontinuous.
maybe discontinuous.
Submitted November 7, 2011. Published February 7, 2012.
Math Subject Classifications: 35J92, 35J70, 35R70
Key Words: p(x)-Laplacian problem; critical Sobolev exponents;
discontinuous nonlinearities.
Show me the PDF file (268 KB),
TEX file for this article.
 |
Xudong Shang
School of Mathematics
Nanjing Normal University Taizhou College
225300, Jiangsu, China
email: xudong-shang@163.com
|
|---|
 |
Zhigang Wang
School of Mathematics
Nanjing Normal University Taizhou College
225300, Jiangsu, China
email: wzg19.scut@163.com
|
|---|
Return to the EJDE web page
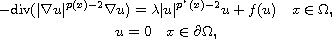
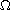 is a smooth bounded domain in
is a smooth bounded domain in
 ,
,
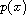 is a continuous function with
is a continuous function with
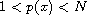 and
and
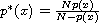 .
Applying nonsmooth critical point theory for locally Lipschitz functionals,
we show that there is at least one nontrivial solution when
.
Applying nonsmooth critical point theory for locally Lipschitz functionals,
we show that there is at least one nontrivial solution when
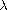 less than a certain number, and
less than a certain number, and
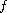 maybe discontinuous.
maybe discontinuous.

