Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 33, pp. 1-9.
Multiple solutions for semilinear elliptic equations
with nonlinear boundary conditions
Junichi Harada, Mitsuharu Otani
Abstract:
We consider the elliptic problem with nonlinear boundary conditions:

where
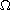 is a bounded domain in
is a bounded domain in
 .
Proving the existence of solutions of this problem relies
essentially on a variational argument.
However, since
.
Proving the existence of solutions of this problem relies
essentially on a variational argument.
However, since
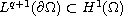 does not hold for large q, the standard variational method can not be
applied directly. To overcome this difficulty, we use approximation methods
and uniform a priori estimates for solutions of approximate equations.
does not hold for large q, the standard variational method can not be
applied directly. To overcome this difficulty, we use approximation methods
and uniform a priori estimates for solutions of approximate equations.
Submitted November 17, 2011. Published February 23, 2012.
Math Subject Classifications: 35J20.
Key Words: Nonlinear boundary conditions
Show me the PDF file (234 KB),
TEX file for this article.
| |
Junichi Harada
Department of Applied Physics
School of Science and Engineering
Waseda University, 3-4-1 Okubo
Shinjuku-ku Tokyo, 169-8555, Japan
email: harada-j@aoni.waseda.jp
|
|---|
 |
Mitsuharu Ôtani
Department of Applied Physics
School of Science and Engineering
Waseda University, 3-4-1 Okubo
Shinjuku-ku Tokyo, 169-8555, Japan
email: otani@waseda.jp
|
|---|
Return to the EJDE web page

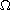 is a bounded domain in
is a bounded domain in
 .
Proving the existence of solutions of this problem relies
essentially on a variational argument.
However, since
.
Proving the existence of solutions of this problem relies
essentially on a variational argument.
However, since
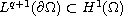 does not hold for large q, the standard variational method can not be
applied directly. To overcome this difficulty, we use approximation methods
and uniform a priori estimates for solutions of approximate equations.
does not hold for large q, the standard variational method can not be
applied directly. To overcome this difficulty, we use approximation methods
and uniform a priori estimates for solutions of approximate equations.
