Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 41, pp. 1-13.
Global solutions in lower order Sobolev spaces for the generalized
Boussinesq equation
Luiz G. Farah, Hongwei Wang
Abstract:
We show that the Cauchy problem for the defocusing generalized Boussinesq
equation
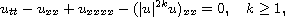
on the real line is globally well-posed in
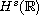 with
s>1-(1/(3k)). To do this, we use the I-method, introduced by
Colliander, Keel, Staffilani, Takaoka and Tao [8,9],
to define a modification of the energy functional that is almost
conserved in time. Our result extends a previous result obtained
by Farah and Linares [16] for the case k=1.
with
s>1-(1/(3k)). To do this, we use the I-method, introduced by
Colliander, Keel, Staffilani, Takaoka and Tao [8,9],
to define a modification of the energy functional that is almost
conserved in time. Our result extends a previous result obtained
by Farah and Linares [16] for the case k=1.
Submitted October 3, 2011. Published March 16, 2012.
Math Subject Classifications: 35B30, 35Q55.
Key Words: Boussinesq equation; global well-posedness; I-method.
Show me the PDF file (273 KB),
TEX file for this article.
 |
Luiz G. Farah
ICEx, Universidade Federal de Minas Gerais
Av. Ant&ocric;nio Carlos, 6627, Caixa Postal 702, 30123-970
Belo Horizonte-MG, Brazil
email: lgfarah@gmail.com
|
|---|
 |
Hongwei Wang
Faculty of Science, Xi'an Jiaotong University
Xi'an 710049, China
Department of Mathematics, Xinxiang College
Xinxiang 453003, China
email: wang.hw@stu.xjtu.edu.cn
|
|---|
Return to the EJDE web page
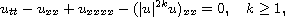
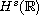 with
s>1-(1/(3k)). To do this, we use the I-method, introduced by
Colliander, Keel, Staffilani, Takaoka and Tao [8,9],
to define a modification of the energy functional that is almost
conserved in time. Our result extends a previous result obtained
by Farah and Linares [16] for the case k=1.
with
s>1-(1/(3k)). To do this, we use the I-method, introduced by
Colliander, Keel, Staffilani, Takaoka and Tao [8,9],
to define a modification of the energy functional that is almost
conserved in time. Our result extends a previous result obtained
by Farah and Linares [16] for the case k=1.

