Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 58, pp. 1-9.
Existence of bounded positive solutions of a nonlinear
differential system
Sabrine Gontara
Abstract:
In this article, we study the existence and nonexistence of solutions for the
system
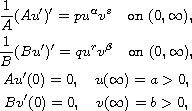
where
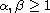 ,
,
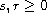 , p,q are two nonnegative
functions on
, p,q are two nonnegative
functions on
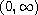 and A, B satisfy appropriate conditions.
Using potential theory tools, we show the existence of a positive
continuous solution. This allows us to prove the existence of entire
positive radial solutions for some elliptic systems.
and A, B satisfy appropriate conditions.
Using potential theory tools, we show the existence of a positive
continuous solution. This allows us to prove the existence of entire
positive radial solutions for some elliptic systems.
Submitted January 20, 2012. Published April 10, 2012.
Math Subject Classifications: 35J56, 31B10, 34B16, 34B27.
Key Words: Nonlinear equation; Green's function; asymptotic behavior;
singular operator; positive solution.
Show me the PDF file (208 KB),
TEX file for this article.
 |
Sabrine Gontara
Dépatement de mathématiques
Faculté des sciences de Tunis
Campus Universitaire, 2092 Tunis, Tunisia
email: sabrine-28@hotmail.fr
|
|---|
Return to the EJDE web page
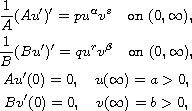
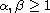 ,
,
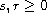 , p,q are two nonnegative
functions on
, p,q are two nonnegative
functions on
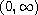 and A, B satisfy appropriate conditions.
Using potential theory tools, we show the existence of a positive
continuous solution. This allows us to prove the existence of entire
positive radial solutions for some elliptic systems.
and A, B satisfy appropriate conditions.
Using potential theory tools, we show the existence of a positive
continuous solution. This allows us to prove the existence of entire
positive radial solutions for some elliptic systems.
