Electron. J. Diff. Equ.,
Vol. 2012 (2012), No. 85, pp. 1-36.
Existence and concentration of semiclassical states
for nonlinear Schrodinger equations
Shaowei Chen
Abstract:
In this article, we study the semilinear Schrodinger equation
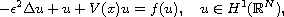
where
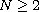 and
and
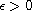 is a small parameter.
The function
is a small parameter.
The function
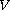 is bounded in
is bounded in
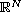 ,
,
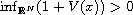 and it has a possibly degenerate
isolated critical point. Under some conditions on f, we prove
that as
and it has a possibly degenerate
isolated critical point. Under some conditions on f, we prove
that as
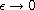 ,
this equation has a solution which concentrates
at the critical point of V.
,
this equation has a solution which concentrates
at the critical point of V.
Submitted August 16, 2011. Published May 31, 2012.
Math Subject Classifications: 35J20, 35J70.
Key Words: Semilinear Schrodinger equation; variational reduction method.
Show me the PDF file (476 KB),
TEX file for this article.
 |
Shaowei Chen
School of Mathematical Sciences
Capital Normal University
Beijing 100048, China
email: chensw@amss.ac.cn
|
|---|
Return to the EJDE web page
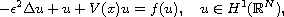
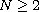 and
and
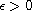 is a small parameter.
The function
is a small parameter.
The function
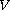 is bounded in
is bounded in
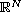 ,
,
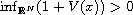 and it has a possibly degenerate
isolated critical point. Under some conditions on f, we prove
that as
and it has a possibly degenerate
isolated critical point. Under some conditions on f, we prove
that as
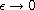 ,
this equation has a solution which concentrates
at the critical point of V.
,
this equation has a solution which concentrates
at the critical point of V.
