Electron. J. Diff. Equ., Vol. 2012 (2012), No. 95, pp. 1-11.

Multiple symmetric positive solutions to four-point boundary-value problems of differential systems with p-Laplacian

Hanying Feng, Donglong Bai, Meiqiang Feng

Abstract:
In this article, we study the four-point boundary-value problem with the one-dimensional p-Laplacian
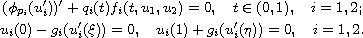
$$\displaylines{ (\phi_{p_i}(u_i'))'+q_i(t)f_i(t,u_1,u_2)=0,\quad t\in(0,1),\quad i=1,2;\cr u_i(0)-g_i(u_i'(\xi))=0,\quad u_i(1)+g_i(u_i'(\eta))=0, \quad i=1,2. }$$
We obtain sufficient conditions such that by means of a fixed point theorem on a cone, there exist multiple symmetric positive solutions to the above boundary-value problem. As an application, we give an example that we illustrates our results.

Submitted March 9, 2012. Published June 10, 2012.
Math Subject Classifications: 34B10, 34B15, 34B18.
Key Words: Four-point boundary-value problem; differential system; fixed point theorem; symmetric positive solution; one-dimensional p-Laplacian

Show me the PDF file (237 KB), TEX file, and other files for this article.

Hanying Feng
Department of Mathematics
Shijiazhuang Mechanical Engineering College
Shijiazhuang 050003, China
email: fhanying@yahoo.com.cn
Donglong Bai
Department of Mathematics
Shijiazhuang Mechanical Engineering College
Shijiazhuang 050003, China
email: baidonglong@yeal.net
Meiqiang Feng
School of Applied Science
Beijing Information Science and Technology University
Beijing 100092, China
email: meiqiangfeng@sina.com

Return to the EJDE web page