Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 06, pp. 1-6.
Asymptotically periodic solutions for differential and
difference inclusions in Hilbert spaces
Gheorghe Morosanu, Figen Ozpinar
Abstract:
Let
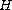 be a real Hilbert space and let
be a real Hilbert space and let
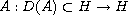 be a
(possibly set-valued) maximal monotone operator. We
investigate the existence of asymptotically periodic solutions to
the differential equation (inclusion)
be a
(possibly set-valued) maximal monotone operator. We
investigate the existence of asymptotically periodic solutions to
the differential equation (inclusion)
 ,
,
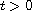 ,
where
,
where
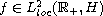 is a
is a
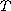 -periodic
function (
-periodic
function (
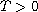 )
and
)
and
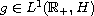 . Consider also the
following difference inclusion (which is a discrete analogue of the
above inclusion):
. Consider also the
following difference inclusion (which is a discrete analogue of the
above inclusion):
 ,
where
,
where
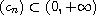 ,
,
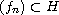 are
are
 -periodic sequences for a positive integer
-periodic sequences for a positive integer
 and
and
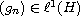 .
We investigate the weak or strong
convergence of its solutions to
.
We investigate the weak or strong
convergence of its solutions to
 -periodic sequences. We show that
the previous results due to Baillon, Haraux (1977) and
Djafari Rouhani, Khatibzadeh (2012) corresponding to
-periodic sequences. We show that
the previous results due to Baillon, Haraux (1977) and
Djafari Rouhani, Khatibzadeh (2012) corresponding to
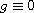 ,
respectively
,
respectively
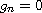 ,
,
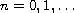 , remain valid for
, remain valid for
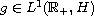 , respectively
, respectively
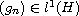 .
.
Submitted October 18, 2012. Published January 8, 2013.
Math Subject Classifications: 39A10, 39A11, 47H05, 34G25.
Key Words: Differential inclusion; difference inclusion; subdifferential;
maximal monotone operator; weak convergence; strong convergence.
Show me the PDF file (190 KB),
TEX file for this article.
 |
Gheorghe Morosanu
Department of Mathematics and its Applications
Central European University
Budapest, Hungary
email: morosanug@ceu.hu
|
|---|
 |
Figen Ozpinar
Bolvadin Vocational School
Afyon Kocatepe University
Afyonkarahisar, Turkey
email: fozpinar@aku.edu.tr
|
|---|
Return to the EJDE web page
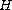 be a real Hilbert space and let
be a real Hilbert space and let
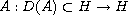 be a
(possibly set-valued) maximal monotone operator. We
investigate the existence of asymptotically periodic solutions to
the differential equation (inclusion)
be a
(possibly set-valued) maximal monotone operator. We
investigate the existence of asymptotically periodic solutions to
the differential equation (inclusion)
 ,
,
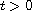 ,
where
,
where
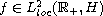 is a
is a
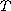 -periodic
function (
-periodic
function (
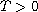 )
and
)
and
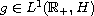 . Consider also the
following difference inclusion (which is a discrete analogue of the
above inclusion):
. Consider also the
following difference inclusion (which is a discrete analogue of the
above inclusion):
 ,
where
,
where
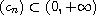 ,
,
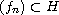 are
are
 -periodic sequences for a positive integer
-periodic sequences for a positive integer
 and
and
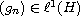 .
We investigate the weak or strong
convergence of its solutions to
.
We investigate the weak or strong
convergence of its solutions to
 -periodic sequences. We show that
the previous results due to Baillon, Haraux (1977) and
Djafari Rouhani, Khatibzadeh (2012) corresponding to
-periodic sequences. We show that
the previous results due to Baillon, Haraux (1977) and
Djafari Rouhani, Khatibzadeh (2012) corresponding to
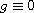 ,
respectively
,
respectively
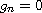 ,
,
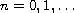 , remain valid for
, remain valid for
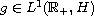 , respectively
, respectively
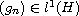 .
.

