Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 114, pp. 1-10.
Existence of exponential attractors for the plate equations
with strong damping
Qiaozhen Ma, Yun Yang, Xiaoliang Zhang
Abstract:
We show the existence of
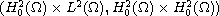 -global
attractors for plate equations with critical nonlinearity when
-global
attractors for plate equations with critical nonlinearity when
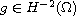 .
Furthermore we prove that for each fixed
.
Furthermore we prove that for each fixed
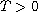 ,
there is an (
,
there is an (
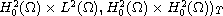 -exponential attractor
for all
-exponential attractor
for all
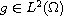 ,
which attracts
any
,
which attracts
any
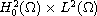 -bounded set under the stronger
-bounded set under the stronger
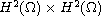 -norm for all
-norm for all
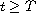 .
.
Submitted November 29, 2012. Published May 6, 2013.
Math Subject Classifications: 35Q35, 35B40, 35B41.
Key Words: Plate equation; critical exponent; exponential attractor.
Show me the PDF file (259 KB),
TEX file for this article.
 |
Qiaozhen Ma
College of Mathematics and Statistics
Northwest Normal University
Lanzhou 730070, China
email: maqzh@nwnu.edu.cn
|
|---|
 |
Yun Yang
College of Mathematics and Statistics
Northwest Normal University
Lanzhou 730070, China
email: yangyun880@163.com
|
|---|
| |
Xiaoliang Zhang
College of Mathematics and Statistics
Northwest Normal University
Lanzhou 730070, China
email: zhangxl258@163.com
|
|---|
Return to the EJDE web page
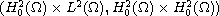 -global
attractors for plate equations with critical nonlinearity when
-global
attractors for plate equations with critical nonlinearity when
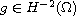 .
Furthermore we prove that for each fixed
.
Furthermore we prove that for each fixed
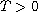 ,
there is an (
,
there is an (
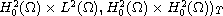 -exponential attractor
for all
-exponential attractor
for all
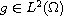 ,
which attracts
any
,
which attracts
any
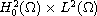 -bounded set under the stronger
-bounded set under the stronger
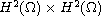 -norm for all
-norm for all
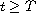 .
.

