Electron. J. Diff. Equ.,
Vol. 2013 (2013), No. 127, pp. 1-11.
Ground states for the fractional Schrodinger equation
Binhua Feng
Abstract:
In this article, we show the existence of ground state solutions
for the nonlinear Schrodinger equation with fractional Laplacian

We use the concentration compactness principle in fractional
Sobolev spaces
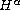 for
for
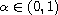 .
Our results generalize the corresponding results in the case
.
Our results generalize the corresponding results in the case
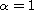 .
.
Submitted November 2, 2012. Published May 27, 2013.
Math Subject Classifications: 35J60, 35Q55.
Key Words: Fractional Laplacians; nonlinear Schrodinger equation;
ground states; concentration compactness.
Show me the PDF file (240 KB),
TEX file for this article.
 |
Binhua Feng
School of Mathematics and Statistics, Lanzhou University
Lanzhou 730000, China
Tel: +86-0931-8912483; Fax: +86-0931-8912481
email: binhuaf@163.com
|
|---|
Return to the EJDE web page

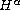 for
for
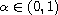 .
Our results generalize the corresponding results in the case
.
Our results generalize the corresponding results in the case
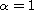 .
.
